C语言最短路径算法(Floyd算法)
更高类别:[C 语言] C 语言目录
1. 各种距离概念
4. 【示例3:C语言实现的最短路径算法】(#4-example-3-shortest-path-algorithm-implemented-in-c-language)
a. GitHub
1.(参考)各种距离概念
⑴ 距离函数:定义距离
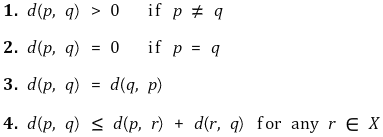
⑵ 类型1: L1距离
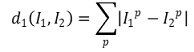
⑶ 类型2: L2距离:使用勾股定理的欧氏距离(标准)
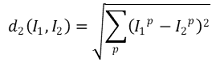
⑷ 类型3: p-范数
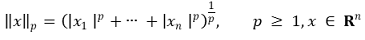 </中心>
</中心>⑸ 类型4:点积
⑹ 类型5: linkage metric:定义簇之间的距离
⑺ 类型 6: [KL距离](https://jb243.github.io/pages/2145#:~:text=%E2%91%A7-,%EC%83%81%EB%8C%80%20%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC,-(相对%20熵%2C)(Kullback-Leibler散度)
⑻ 类型 7: 汉明距离:通过为每个数据点指定二进制值来测量数据点之间的距离
⑼ 类型8: 马氏距离:衡量数据的分布情况
2.示例 1:使用贝尔曼方程的最短路径算法
考虑一个有根二叉树网络。每个内部节点 x 有两个子节点,分别表示为 x(lhs) 和 x(rhs)。从 x 移动到其子节点 x(a) 的成本为 la,其中 a ∈ {lhs,rhs}。对于每个节点 x,令 Lx 为从 x 到叶节点的任何路径的最小成本。对于每个叶节点 y,定义 Ly = 0。表明对于任何内部节点 x,以下内容成立:
证明可以在此链接中找到。
3.示例 2:Dijkstra 算法
⑴ 问题:下图展示了一个带有顶点集(V={A,B,C,D,E,F,G,H})的有向加权图。使用 Dijkstra 算法,找到从顶点 A 到顶点 H 的最短距离和最短路径。
⑵ 解决办法
① 初始化
○ d[A]=0, 且所有其他 d[·] = ∞
② 从A开始,松弛相邻顶点
○ d[B] = 7, d[D] = 8, d[C] = 12> ③ 未访问过的顶点中,当前最小值为B(7)→从B开始松弛
○ (d[D] = min(当前 d[D], d[B] + 5) = 当前 d[D] = 8) → 无改善
○ d[E] = min(当前 d[E], d[B] + 9) = d[B] + 9 = 16 → 更新为 16
④ 未访问顶点中,当前最小值为D(8)→从D开始松弛
○ d[E] = min(当前 d[E], d[D] + 2) = d[D] + 2 = 10 → 更新为 10
○ d[G] = min(当前 d[G], d[D] + 14) = d[D] + 14 = 22 → 更新为 22
○ d[C] = min(当前 d[C], d[D] + 5) = 当前 d[C] = 12 → 无改善
⑤ 未访问顶点中,当前最小值为E(10) → 从E开始松弛
○ d[H] = min(当前 d[H], d[E] + 3) = d[E] + 3 = 13 → 更新为 13
⑥ 未访问顶点中,当前最小值为C(12),但(d[H])没有提高
⑦ 未访问顶点中,当前最小值为目标顶点H,因此(d[H])最终确定→停止
⑧ 结论
○ 最短距离:13
○ 最短路径:A → D → E → H
4. C语言实现的最短路径算法
⑴问题情况:比如从0到5的路径需要花费6,也就是说需要移动6的距离。
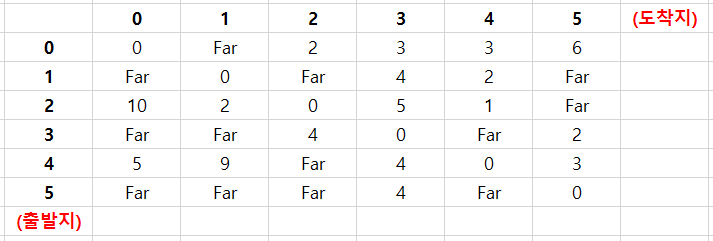
表1.问题情况
⑵ Dijkstra算法:特点是for短语的两层嵌套
受保护_0
⑶弗洛伊德算法(Floyd–Warshall):特点是三重嵌套的for循环。比 Dijkstra 算法更直观。
受保护_1
输入:2013 年 12 月 13 日 22:55