Korean, Edit

第 4 章。张力和压力（应力和应变）

更高类别： 【材料力学】【材料力学目录】(https://jb243.github.io/pages/218)

1. 计算轴向应力

2. 载荷变形曲线

3. 各种压力

1.计算轴向应力

⑴ 拉、压

⑵ 在水平面内旋转的薄环产生的拉应力

</中心>

2. 载荷-变形曲线（应变-应力曲线）

⑴ 概述

① 载荷-变形曲线

○ X 轴 : 应变

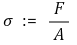</中心>

○ Y 轴 : 应力

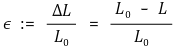
○ 以下区域： 能源

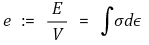
② 压缩试验装置

○ 载荷-变形曲线通常是通过压缩试验而不是拉伸试验获得的

○ 压缩试验设备通常采用万能试验机（UTM）

○ 硬质样品 : 将十字头的下降速度设置为约 1.23 mm/min ± 50%

○ 软样品 : 将十字头的下降速度设置为约 2.5-30 mm/min ± 50%

⑵ 弹性区

①定义：可通过弹性恢复的形变范围

② 比例限制

○ 定义 : 胡克定律成立时的变形范围

○ 胡克定律 : σ = Eε。 σ：应力。 E：弹性模量。 ε : 应变

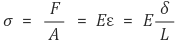
○ 弹性模量（杨氏模量、弹性模量）

○ 从0到比例极限有一个常数值

○ 物体越硬，E值越大，越不易变形

○ 表观弹性模量

○ 初始切线模数 : 原点处切线的斜率»> ○ 割线模数 : 通过原点的直线的平均斜率

○ 切线模数 : 任意点切线的斜率

○ 由赫兹接触理论导出的弹性模量公式

</中心>

○ 弹性程度

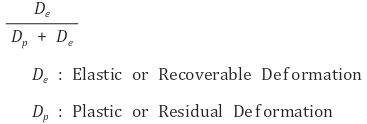
○ 弹性：应力-应变曲线下达到比例极限的面积。变形能的度量之一

○ 如果未定义比例极限，有时将其定义为屈服点之前的面积

○ 示例：

○ 水平刚性梁_ABCD_ 由垂直杆_BE_ 和_CF_ 支撑，并由分别作用于点_A_ 和_D_ 的垂直力_P1_ = 400 kN 和_P2_ = 360 kN 加载（见图）。棒材 BE 和 CF 由钢 (E = 200 GPa) 制成，横截面积为 BE = 11,100 mm² 和 CF = 9,280 mm²。图中显示了条形图上各个点之间的距离。分别确定点 A 和 D 的垂直位移 δA 和 δD。

③ 屈服点

○ 弹性区末端：屈服点后，开始出现微损伤，材料无法恢复到原始状态。

○ 负载暂时不增加的点。

○ 粗糙度 ： 达到屈服点所需的能量。

○ 刚度 ： 从 0 到屈服点的平均斜率。

○ 屈服变形：从0到屈服点的变形。

④ 迟滞

○ 滞后现象：材料的物理量不仅由其当前状态决定，还由状态变化过程决定的现象。

○ 应力-应变曲线的滞后现象：超过屈服点的变形，即使去除载荷后也不会恢复到原始状态的现象。

○ 机械迟滞：加载时吸收的能量和卸载时释放的能量。

○ 机械滞后用每单位体积的功量（J/m3）表示。

○ 磁滞损耗：加载时机械磁滞与吸收能量的比值，以百分比表示。

⑶ 塑性区域

①定义：不能通过弹性恢复的变形范围。

② 弹性和非弹性应变能

○ 在弹性限度内：恢复全部能量。

○ 超出弹性极限：仅恢复与新弹性范围相关的能量。

③ 破裂或断裂

○ 定义 ： 物体被完全破坏的点。

○ 韧性 : 达到最终破裂点所需的能量。

○变形破裂：从0变形到最终破裂点。

○ 断裂强度：断裂瞬间作用于材料的应力。

④极限应力：屈服点与最终断裂点之间的最大应力。

○ 一般指最终破裂点的应力。

○ 强度：物体的极限应力。

⑤ 延展性和脆性：差异程度» ○ 延展性：从屈服点到最终断裂点需要大量变形的特性。

○ 延展性材料沿断裂面发生显着变形。

○ 脆性：从屈服点到最终破裂点需要有少量变形的性质。

○ 脆性材料沿断裂面的变形最小。

⑷ 疲劳

① 定义：材料在一定时间后被破坏的现象，即使受到低于断裂应力的应力。

② 循环疲劳

③ 具有粘弹性的材料具有随时间变化的应力-载荷关系。

○ 用流变模型解释。

○ 应力松弛 : 当应变保持恒定时应力减小的现象。

○ 蠕变现象 ： 如果载荷持续时间较长，即使在低于屈服点的小载荷下也会发生损坏的现象。

⑸ 泊松比

①定义：横向应变与纵向应变之比。

○ 泊松比始终为正。

○ 值取决于晶体结构。

○ 泊松比始终小于 0.5。

○ 对于金属，一般为1/3左右。

② 截面积的变化：用泊松比ν表示，

③体积变化：通过叠加原理获得。

○ 配方

○ 通过延伸特定截面的晶体结构，可以测定体积应变ε_V。

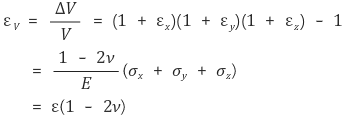
○ 体积应变ε_V也可近似表示为：

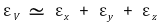
○ 膨胀时体积不能出现负变化。

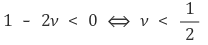
○ 然而，橡胶的泊松比ν为0.5，因此体积没有变化。

④ 纵向弹性模量E与剪切模量G的关系

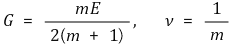
3。各种压力

⑴ 偏心加载单杆

① 最大应力：注意M代表绕重心的力矩。

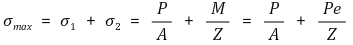
② 最小应力：注意M代表绕重心的力矩。

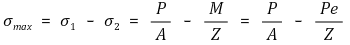
③ 偏心率：偏心率e是最小应力变为0的距离。

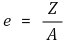
⑵ 立柱

①欧拉屈曲载荷：也称为临界载荷或安全载荷。

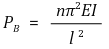
○ n：末端固定系数。值越高表示色谱柱越强。

○ ℓ：柱的长度。长度越长表示色谱柱越弱。

○ 注：EI 通常附有。

② 欧拉屈曲应力：

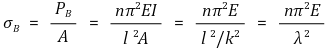
○ k：回转半径（最小截面面积二阶矩）

○ λ：长细比

③长细比：又称有效长细比。

⑶ 热应力

① 热膨胀：当部件温度升高时，由于动能增加，其长度在各个方向上增加。

○ 线膨胀系数α与温度变化ΔT：线状物体的长度ℓ = ℓ₀ (1 + α ΔT)。

○ 体积膨胀系数β和温度变化ΔT：物体的总体积V = V₀ (1 + β ΔT)。

○ β ≒ 3α 大约成立： 1 + β ΔT = (1 + α ΔT)³ ≒ 1 + 3α ΔT （证明）

○ 热膨胀系数：Zn、Pb、Mg ＞ W、Mo ＞ V

② 热应力：元件发生热膨胀但两点之间的距离不变时产生的应力。

⑷ 脉冲应力

① 公式： 注： 需要记忆。

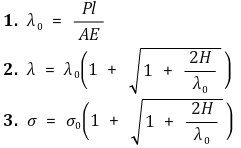
② 当没有初速度的情况下突然施加力时，σ = 2σ0：将H = 0 代入方程。

⑸ 不确定

① 示例

○ 图中所示的轴向负载杆_ABCD_ 固定在刚性支架之间。该杆的横截面积为 A₁（从 A 到 C）和 2A₁（从 C 到 D）。确定条形两端的反应 R_A 和 R_D。

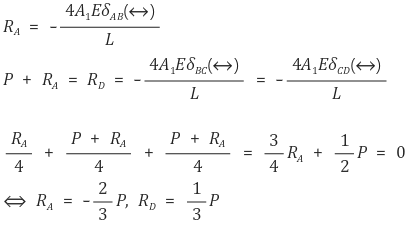
输入： 2016.04.24 16:32

修改： 2020.06.30 21:33