Chapter 3-1. Inclusion-Exclusion Principle
Higher category : 【Statistics】 Chapter 3. Probability Space
1. Intersection and union relationship
2. Inclusion-exclusion principle
1. Intersection and union relationship
⑴ theorem
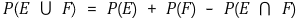
⑵ induction
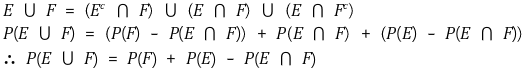
2. Inclusion-exclusion principle
⑴ theorem
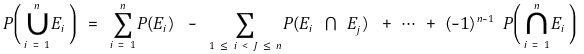
⑵ induction
by the intersection and union relationship, the following equation can be derived
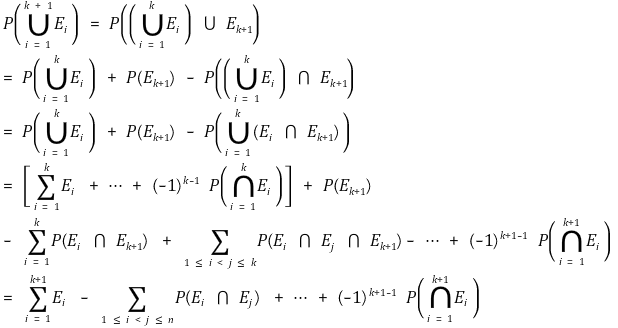
as a result, when the equation is established for n = k, it is also established for n = k+1
the intersection and union relationship shows the equation is established for n=2
in conclusion, the inclusion-exclusion principle is established for all n ∈ ℕ
Input : 2019.06.27 11:33