Chapter 4. Tension and Compression (stress and strain)
Higher category : 【Materials Mechanics】 Materials Mechanics Table of Contents
1. Calculating Axial Stress
⑴ Tension, Compression

⑵ Tensile stress occurring in a thin ring rotating in a horizontal plane


2. Load-Deformation Curve(strain-stress curve)
⑴ Overview
① Load-Deformation Curve

○ X-axis : Strain
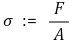
○ Y-axis : Stress
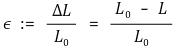
○ Area below : Energy
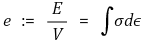
② Compression Testing Device
○ Load-Deformation curves are usually obtained through compression tests rather than tension tests
○ Universal Testing Machine (UTM) is typically used as the compression testing device

○ Hard samples : Set the descent speed of the crosshead to approximately 1.23 mm/min ± 50%
○ Soft samples : Set the descent speed of the crosshead to approximately 2.5-30 mm/min ± 50%
⑵ Elastic Region
① Definition : Range of deformation that can be restored by elasticity
② Proportional Limit
○ Definition : Range of deformation where Hooke’s law holds true
○ Hooke’s law : σ = Eε. σ : Stress. E : Elastic modulus. ε : Strain
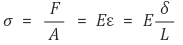
○ Elastic Modulus (Young’s modulus, Modulus of elasticity)
○ It has a constant value from 0 to the proportional limit
○ The harder the object, the larger the E value, and the more difficult it is to deform
○ Apparent modulus of elasticity
○ Initial Tangent Modulus : Slope of the tangent at the origin
○ Secant Modulus : Average slope of the line passing through the origin
○ Tangent Modulus : Slope of the tangent at any point
○ Formula of elastic modulus derived from Hertz’s contact theory

○ Degree of Elasticity

○ Resilience : Area under the stress-strain curve up to the proportional limit. One of the measures of deformation energy
○ If the proportional limit is not defined, it is sometimes defined as the area up to the yield point
○ Example:
○ The horizontal rigid beam ABCD is supported by vertical bars BE and CF and is loaded by vertical forces P1 = 400 kN and P2 = 360 kN acting at points A and D, respectively (see figure). Bars BE and CF are made of steel (E = 200 GPa) and have cross-sectional areas of BE = 11,100 mm² and CF = 9,280 mm². The distance between various points on the bars are shown in the figure. Determine the vertical displacements δA and δD of points A and D, respectively.

③ Yield point
○ End of the elastic region: After the yield point, micro-damage begins and the material cannot return to its original state.
○ Point where the load does not increase temporarily.
○ Roughness : Energy required until the yield point.
○ Stiffness : Average slope from 0 to the yield point.
○ Yield deformation: Deformation from 0 to the yield point.
④ Hysteresis
○ Hysteresis: Phenomenon where the physical quantities of a material are determined not only by its current state but also by the process of state change.
○ Hysteresis of the stress-strain curve: Phenomenon where deformations beyond the yield point do not recover to the original state even after the load is removed.
○ Mechanical hysteresis: Amount of energy absorbed during loading and released during unloading.
○ Mechanical hysteresis is represented by the amount of work per unit volume in J/m³.
○ Hysteresis loss: Ratio of the mechanical hysteresis to the absorbed energy during loading, expressed as a percentage.
⑶ Plastic region
① Definition: Range of deformations that cannot be restored by elasticity.
② Elastic and inelastic strain energy
○ Within the elastic limit: Total energy is restored.
○ Beyond the elastic limit: Only the energy related to the new elastic range is restored.

③ Rupture or fracture
○ Definition : Point at which an object is completely destroyed.
○ Toughness : Energy required until the final rupture point.
○ Rupture of deformation: Deformation from 0 to the final rupture point.
○ Fracture strength: Stress applied to the material at the moment of rupture.
④ Ultimate stress: Maximum stress between the yield point and the final rupture point.
○ Generally refers to the stress at the final rupture point.
○ Strength: Ultimate stress of an object.
⑤ Ductility and brittleness: Degree of difference
○ Ductility: Property that requires a significant amount of deformation from the yield point to the final rupture point.
○ Ductile materials undergo significant deformation along the fracture surface.
○ Brittleness: Property that requires a small amount of deformation from the yield point to the final rupture point.
○ Brittle materials undergo minimal deformation along the fracture surface.
⑷ Fatigue
① Definition: Phenomenon where a material is destroyed after a certain period of time, even when subjected to stresses below the fracture stress.
② Cyclic fatigue
③ Materials with viscoelasticity have stress-load relationships that change over time.
○ Explained by the rheological model.
○ Stress relaxation : Phenomenon where stress decreases when strain remains constant.
○ Creep phenomenon : Phenomenon where damage occurs even under small loads below the yield point if the duration of loading is long.
⑸ Poisson’s ratio
① Definition: Ratio of lateral strain to longitudinal strain.
○ Poisson’s ratio is always positive.
○ Value depends on the crystal structure.
○ Poisson’s ratio is always less than 0.5.
○ For metals, it is generally around 1/3.
② Change in cross-sectional area: In terms of Poisson’s ratio ν,
③ Change in volume: Obtained through the principle of superposition.
○ Formulation

○ It is possible to determine the volumetric strain εV by extending the crystal structure of a specific cross-section.
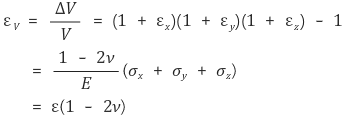
○ Volumetric strain εV can also be expressed approximately as:
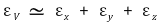
○ Volume cannot have a negative change when subjected to expansion.
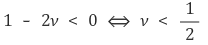
○ However, rubber has a Poisson’s ratio ν of 0.5, so there is no change in volume.
④ Relationship between longitudinal elastic modulus E and shear modulus G
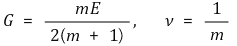
3. Various stresses
⑴ Eccentrically loaded single bar
① Maximum stress: Note that M represents the moment about the center of gravity.
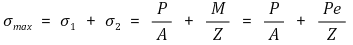
② Minimum stress: Note that M represents the moment about the center of gravity.
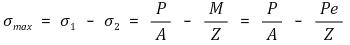
③ Eccentricity: The eccentricity e is the distance where the minimum stress becomes 0.
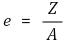
⑵ Column
① Euler’s buckling load: Also known as the critical load or the safe load.
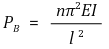
○ n: End-fixity coefficient. A higher value indicates a stronger column.
○ ℓ: Length of the column. A longer length indicates a weaker column.
○ Note: EI is often attached.
② Euler’s buckling stress:
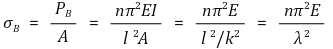
○ k: Radius of gyration (2nd moment of area of the minimum cross-section)
○ λ: Slenderness ratio
③ Slenderness ratio: Also known as the effective slenderness ratio.
⑶ Thermal stress
① Thermal expansion: When the temperature of a component increases, its length increases in all directions due to increased kinetic energy.
○ Linear expansion coefficient α and temperature change ΔT: Length ℓ = ℓ0 (1 + α ΔT) for a linear object.
○ Volumetric expansion coefficient β and temperature change ΔT: Total volume V = V0 (1 + β ΔT) for an object.
○ β ≒ 3α holds approximately: 1 + β ΔT = (1 + α ΔT)3 ≒ 1 + 3α ΔT (proof)
○ Thermal expansion coefficient: Zn, Pb, Mg > W, Mo > V
② Thermal stress: Stress that occurs when a component undergoes thermal expansion but the distance between two points cannot change.

⑷ Impulse stress
① Formulation: Note: Memorization is required.
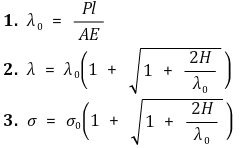
② When the force is applied suddenly without initial velocity, σ = 2σ0: Substitute H = 0 into the equation.
⑸ Indeterminate
① Example
○ The axially loaded bar ABCD shown in the figure is held between rigid supports. The bar has a cross-sectional area A1 from A to C and 2A1 from C to D. Determine the reactions RA and RD at the ends of the bar.

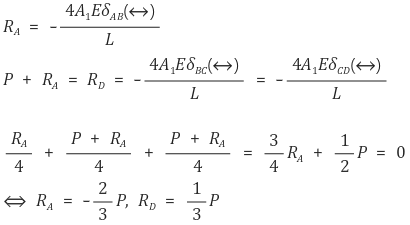
Input: 2016.04.24 16:32
Revised: 2020.06.30 21:33