Chapter 11. Reinforcement Learning
Recommended Reading: 【Algorithm】 Algorithm Index
1. Overview
2. Markov Chain
1. Overview
⑴ Definition
① Supervised Learning
○ Data: (x, y) (where x is a feature, y is a label)
○ Goal: Compute the mapping function x → y
② Unsupervised Learning
○ Data: x (where x is a feature and there is no label)
○ Goal: Learn the underlying structure of x
③ Reinforcement Learning
○ Data: (s, a, r, s’) (where s is state, a is action, r is reward, s’ is the next state)
○ Goal: Maximize the total reward over multiple time steps
① Element 1. State
② Element 2. Reward
○ Definition: The change in the state.
○ Value function: The expected value of future rewards, expressed as lifetime value (VLT).
○ Formulation: For a state s, a policy π, and a discount factor γ that adjusts future value to present value.
○ Provides the basis for choosing an action by evaluating whether a state is good or bad.
③ Element 3. Action
④ Element 4. Policy
○ Definition: The agent’s behavior; a mapping that takes a state as input and outputs an action.
○ Decision process: A general framework for decision-making problems in which states, actions, and rewards unfold over a process.
○ Type 1: Deterministic policy
○ Type 2: Stochastic policy
○ Reason 1: In learning, the optimal behavior is unknown, so exploration is needed.
○ Reason 2: The optimal situation itself may be stochastic (e.g., rock–paper–scissors, or when an opponent exploits determinism).
⑤ Element 5. Model
○ Definition: The behavior/dynamics of the environment.
○ Given a state and an action, the model determines the next state and the reward.
○ Note the distinction between model-free and model-based methods.
⑶ Characteristics: Different from supervised learning and unsupervised learning
① Implicitly receives correct answers: Provided in the form of rewards
② Needs to consider interaction with the environment: Delayed feedback can be an issue
③ Previous decisions influence future interactions
④ Actively gathers information: Reinforcement learning includes the process of obtaining data
2. Markov Chain
⑴ Overview
① Definition: A system where the future state depends only on the current state and not on past states
② A Markov chain refers to a Markov process whose state space is finite or countably infinite.
③ Lemma 1. Chapman-Kolmogorov decomposition
④ Lemma 2. Linear state-space model
① Strongly Connected (= Irreducible): A state where any node i in the graph can reach any other node j
② Period: The greatest common divisor of all paths returning to node i
○ Example: If two nodes A and B are connected as A=B with two edges, the period of each node is 2
③ Aperiodic: When all nodes have a period of 1
○ Aperiodic ⊂ Irreducible
○ Example: If each node has a walk returning to itself, it is aperiodic
④ Stationary State: If $Pr(x_n \mid x_{n-1})$ is independent of $n$, the Markov process is stationary (time-invariant)
⑤ Regular
○ Regular ⊂ Irreducible
○ If there exists a natural number k such that all elements of the k-th power of the transition matrix M^k are positive (i.e., nonzero)
⑥ Lemma 1. Perron-Frobenius theorem
⑦ Lemma 2. Lyapunov equation
⑧ Lemma 3. Bellman equation
⑵ Type 1. Two-State Markov Chain
Figure 1. Two-Scale Markov Chain
① M: Transformation causing state transition in one step
② Mn: Transformation causing state transition in n steps
③ Steady-State Vector: A vector q satisfying Mq = q, i.e., an eigenvector with eigenvalue 1
⑶ Type 2. HMM (Hidden Markov Model)
① χ = {Xi} is a Markov process and Yi = ϕ(Xi) (where ϕ is a deterministic function), then y = {Yi} is a Hidden Markov Model.
② Baum-Welch Algorithm
○ Purpose: Learning HMM parameters
○ Input: Observed data
○ Output: State transition probabilities and emission probabilities of HMM
○ Principle: A type of EM (Expectation Maximization) algorithm
○ Formula
○ Akl: Number of transition from state k to l
○ Ek(b): Number of emissions of observation b from state k
○ Bk: Initial probability for state k
○ Purpose: Find the most likely hidden state sequence given an HMM
○ Input: HMM parameters and observed data
○ N: Number of possible hidden states
○ T: Length of observed data
○ A: State transition probability, akl = probability of transitioning from state k to state l
○ E: Emission probability, ek(x) = probability of observing x in state k
○ B: Initial state probability
○ Output: Most probable state sequence
○ Principle: Uses dynamic programming to compute the optimal path
○ Step 1. Initialization
○ bk: Initial probability of state $k$, $P(s_0 = k)$
○ $e_k(σ)$: Probability of observing the first observation σ in state $k$, $P(x_0 \mid s_0 = k)$
○ Step 2. Recursion
○ Compute maximum probability from the previous state at each time step i = 1, …, T
○ Compute backpointer (ptr) storing the most probable previous state
○ ptri(l) serves to store the previous state k that has the highest probability of transitioning to the current state l.
○ Step 3. Termination
○ Select the highest probability at the final time step
○ Determine the last state of the optimal sequence
○ vk(i - 1): Optimal probability at previous time step i - 1 in state k
○ akl: Probability of transitioning from state k to l
○ Step 4. Traceback
○ Trace back through ptr array from i = T, …, 1 to recover the optimal path
○ Example
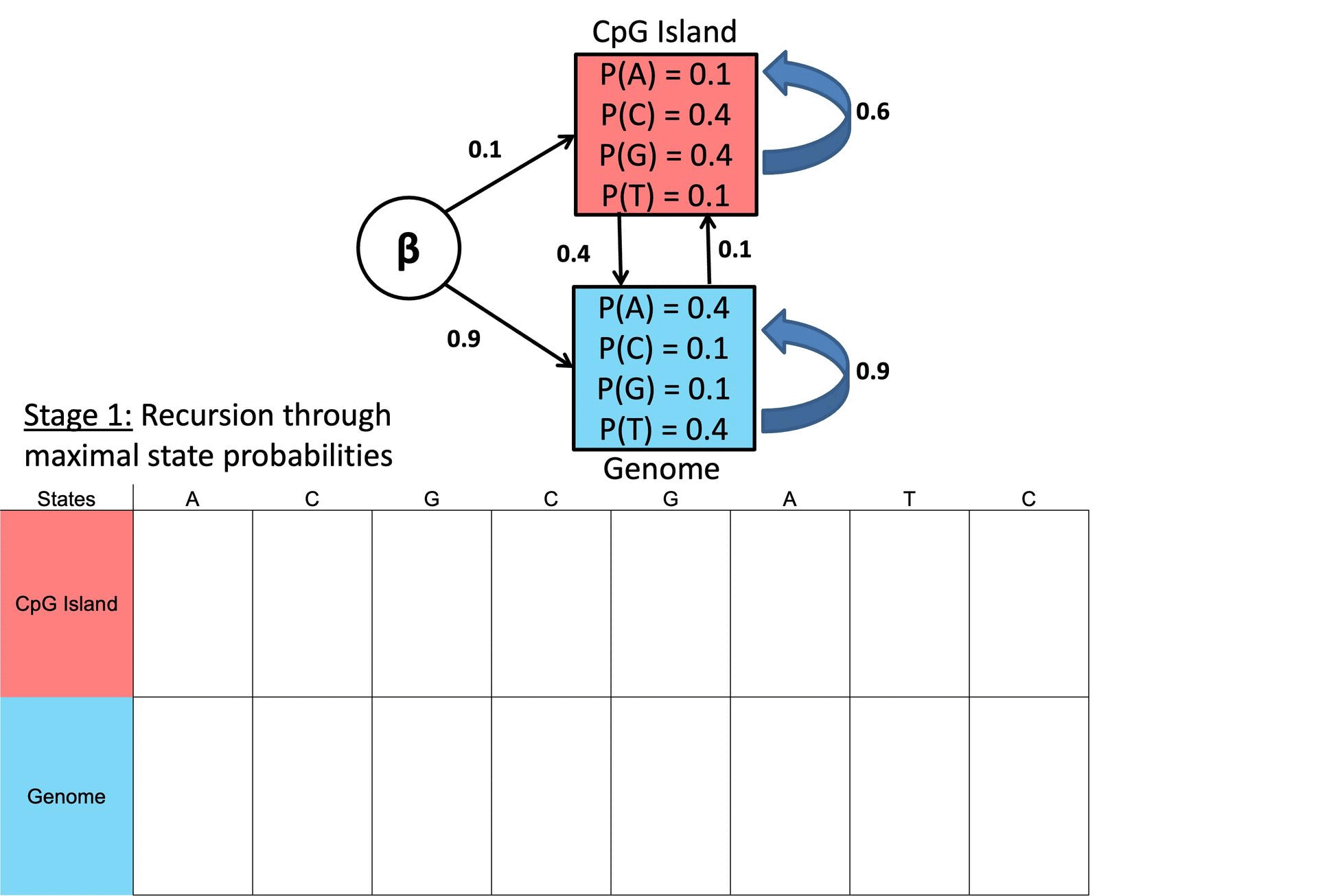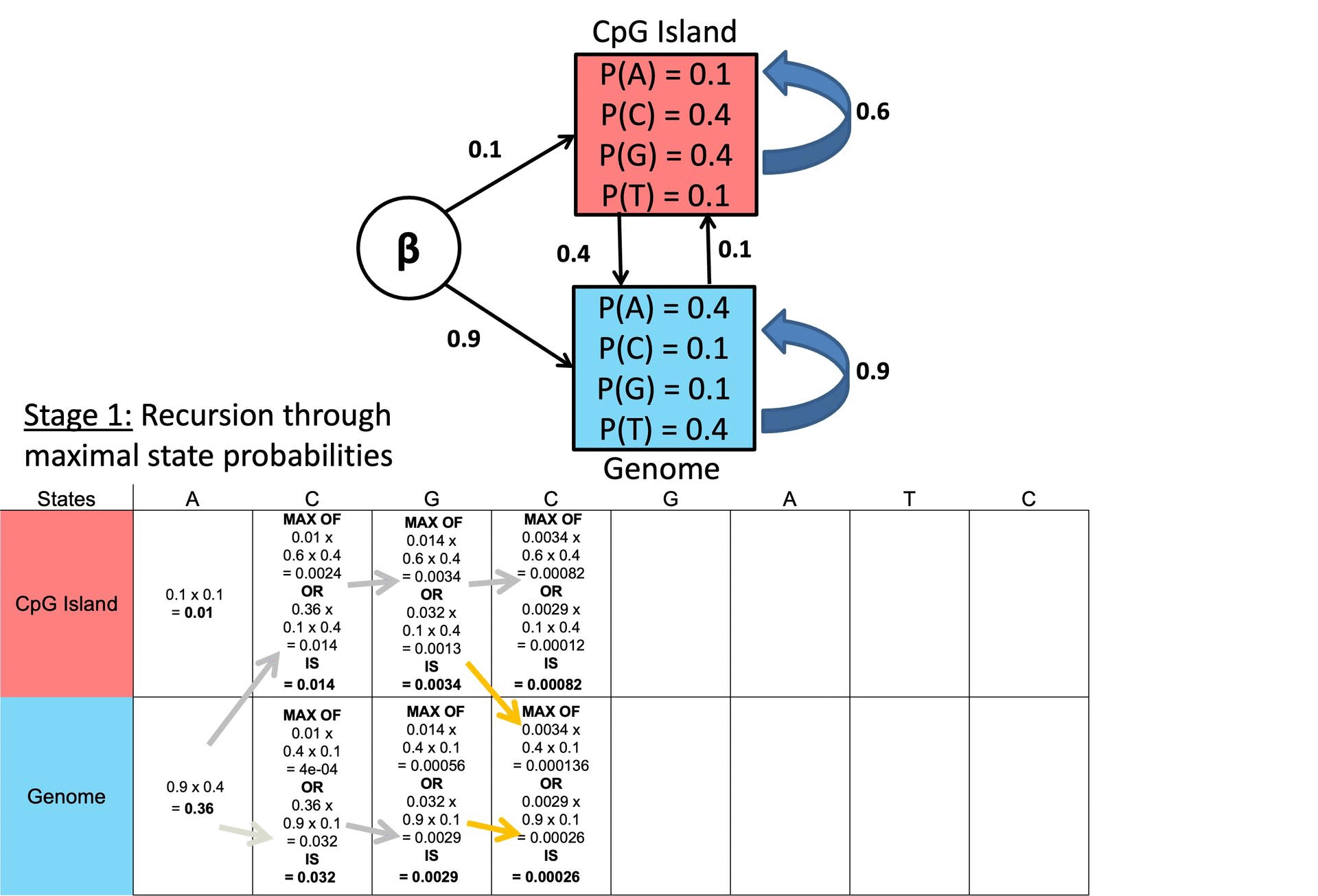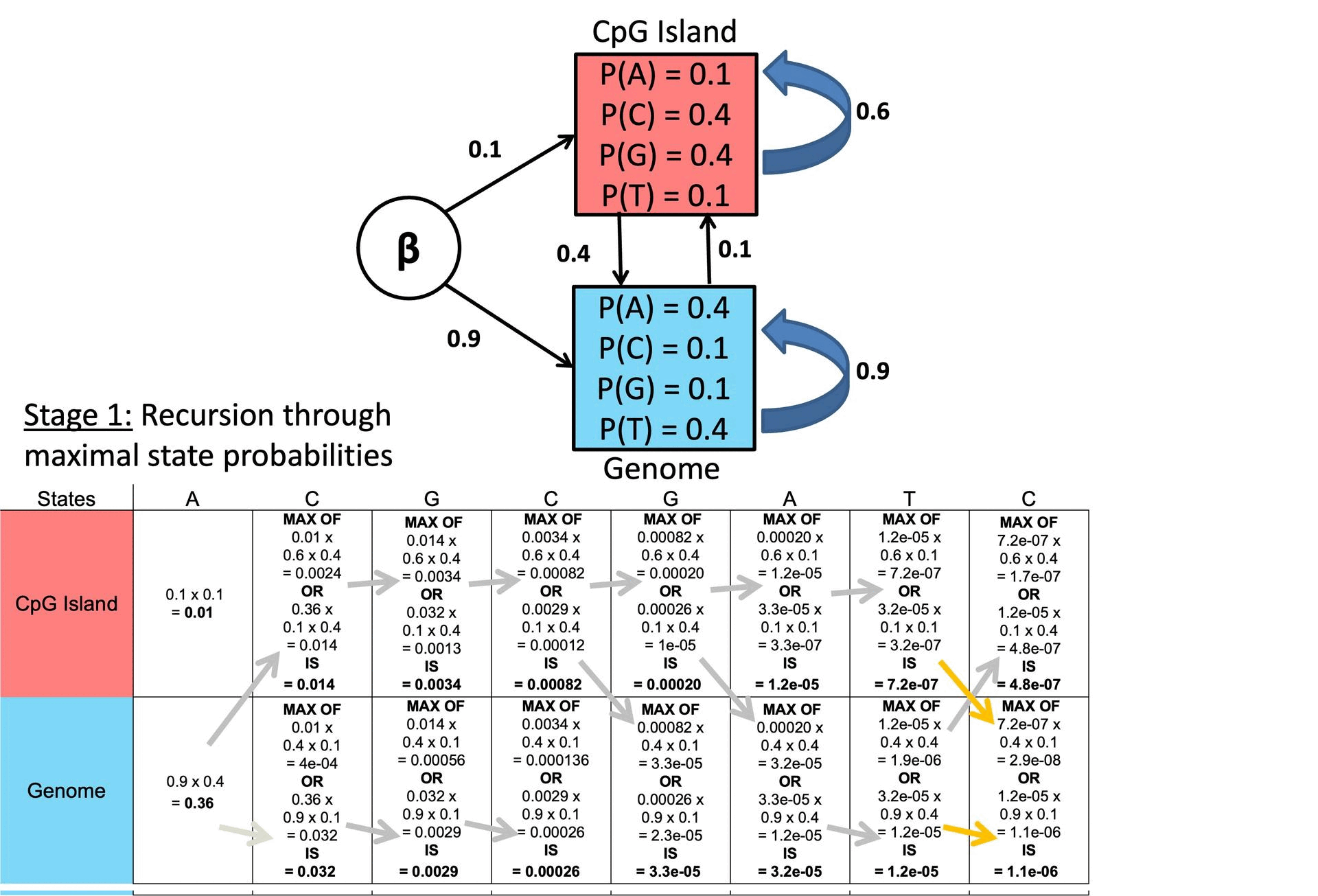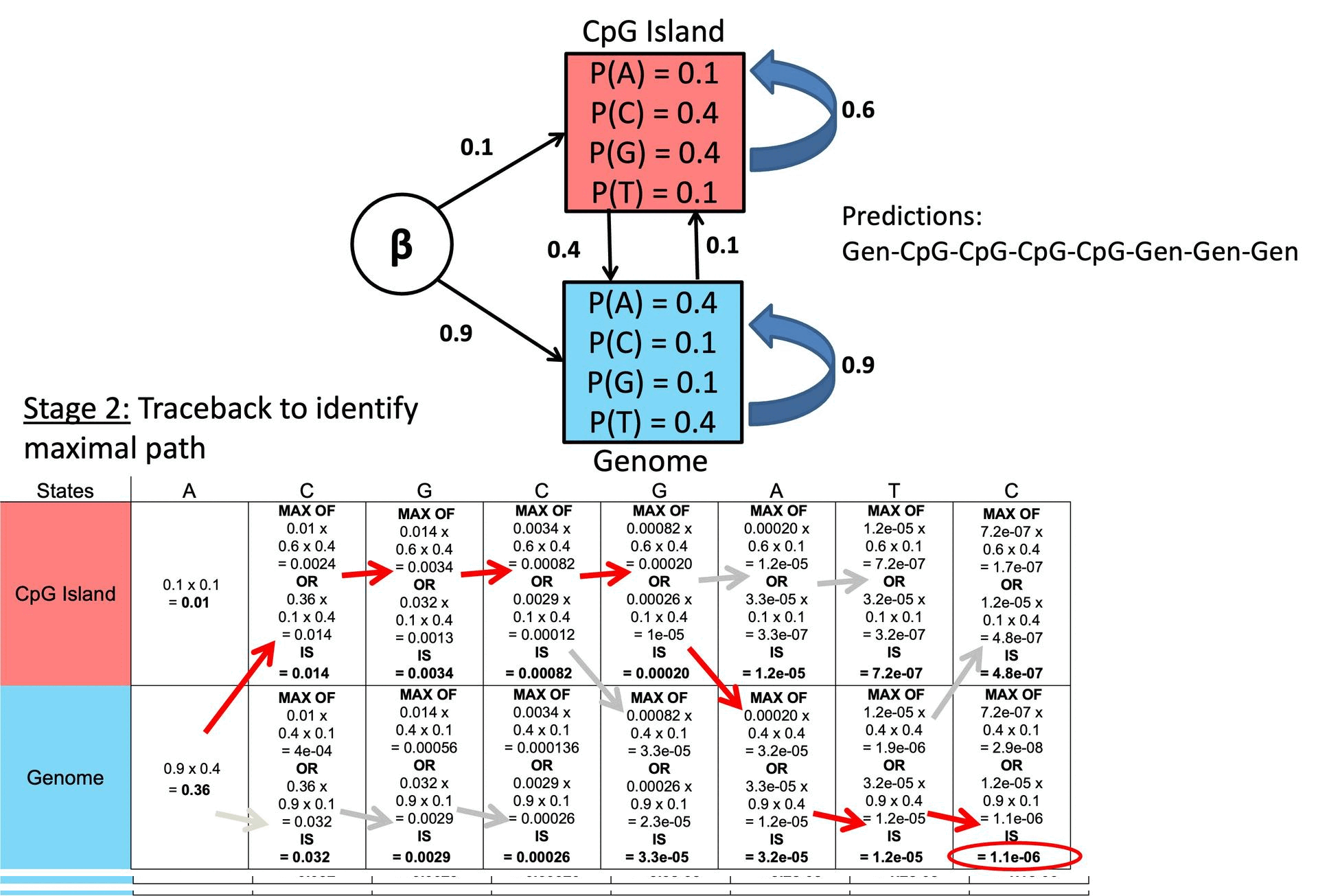
Figure 2. Example of Viterbi Algorithm
○ Python Code
class HMM(object):
def __init__(self, alphabet, hidden_states, A=None, E=None, B=None):
self._alphabet = set(alphabet)
self._hidden_states = set(hidden_states)
self._transitions = A
self._emissions = E
self._initial = B
def _emit(self, cur_state, symbol):
return self._emissions[cur_state][symbol]
def _transition(self, cur_state, next_state):
return self._transitions[cur_state][next_state]
def _init(self, cur_state):
return self._initial[cur_state]
def _states(self):
for k in self._hidden_states:
yield k
def draw(self, filename='hmm'):
nodes = list(self._hidden_states) + ['β']
def get_children(node):
return self._initial.keys() if node == 'β' else self._transitions[node].keys()
def get_edge_label(pred, succ):
return (self._initial if pred == 'β' else self._transitions[pred])[succ]
def get_node_shape(node):
return 'circle' if node == 'β' else 'box'
def get_node_label(node):
if node == 'β':
return 'β'
else:
return r'\n'.join([node, ''] + [
f"{e}: {p}" for e, p in self._emissions[node].items()
])
graphviz(nodes, get_children, filename=filename,
get_edge_label=get_edge_label,
get_node_label=get_node_label,
get_node_shape=get_node_shape,
rankdir='LR')
def viterbi(self, sequence):
trellis = {}
traceback = []
for state in self._states():
trellis[state] = np.log10(self._init(state)) + np.log10(self._emit(state, sequence[0]))
for t in range(1, len(sequence)):
trellis_next = {}
traceback_next = {}
for next_state in self._states():
k={}
for cur_state in self._states():
k[cur_state] = trellis[cur_state] + np.log10(self._transition(cur_state, next_state))
argmaxk = max(k, key=k.get)
trellis_next[next_state] = np.log10(self._emit(next_state, sequence[t])) + k[argmaxk]
traceback_next[next_state] = argmaxk
trellis = trellis_next
traceback.append(traceback_next)
max_final_state = max(trellis, key=trellis.get)
max_final_prob = trellis[max_final_state]
result = [max_final_state]
for t in reversed(range(len(sequence)-1)):
result.append(traceback[t][max_final_state])
max_final_state = traceback[t][max_final_state]
return result[::-1]
④ Type 1. PSSM: Simpler HMM structure
⑤ Type 2. Profile HMM: It is advantageous over PSSMs regarding the following:
○ Diagram of profile HMM
Figure 3. Diagram of profile HMM
○ M, I, and D represent match, insertion, and deletion, respectively.
○ Mi can be transitioned to Mi+1, Ii, and Di+1.
○ Ii can be transitioned to Mi+1, Ii, and Di+1.
○ Di can be transitioned to Mi+1, Ii, and Di+1.
○ Advantage 1. The ability to model insertions and deletion
○ Advantage 2. Transitions are restricted only between valid state traversal.
○ Advantage 3. Boundaries between states are better defined.
⑸ Type 3. Markov chain Monte Carlo (MCMC)
① Definition: A method for generating samples from a Markov chain following a complex probability distribution
② Method 1. Metropolis-Hastings
○ Generate a new candidate sample from the current state → Accept or reject the candidate sample → If accepted, transition to the new state
③ Method 2. Gibbs Sampling
④ Method 3. Importance/Rejection Sampling
⑤ Method 4. Reversible Jump MCMC
○ General MCMC methods like Method 1 and Method 2 sample from a probability distribution in a fixed-dimensional parameter space
○ Reversible Jump MCMC operates in a variable-dimensional parameter space: The number of parameters dynamically changes during sampling
3. Markov Decision Process
⑴ Overview
① Definition: A decision process in which the future depends only on the current state.
② In practice, the vast majority of problem settings can be treated as a Markov decision process (MDP).
③ Schematic: For transitions, the state at t+1 is determined solely as a function of the state at t.
Figure 4. Agent-Environment Interaction in MDP
○ State: $s_t ∈ S$
○ Action: $a_t ∈ A$
○ Reward: $r_t ∈ R(s_t, a_t)$
○ Policy: $a_t ~ π(· \mid s_t)$
○ Transition: $(s_{t+1}, r_{t+1}) ~ P(· \mid s_t, a_t)$
④ Existence of optimal solution $V(s)$
○ Premise 1. Markov property
○ Premise 2. Stationary assumption
○ Premise 3. No distributional shift
⑵ Type 1. Q-learning (Watkins, 1989)
① Overview
○ Learn the Q-function (action-value function) directly from data.
○ Model-free (off-policy), i.e., the transition dynamics $P(x’ \mid x, u)$—is unknown.
○ The reward function $R(s, a)$ is known.
○ Example of value iteration.
② Formula: Because the next state $j$ is fixed, the transition probability term drops out.
○ Step 1. Initialize estimates for all state/action pairs: Q̂(x, u) = 0
○ Step 2. Take a random action $u$
○ Step 3. Observe the next state $x’$ and receive $R(x’, u)$ from the environment: Note that this is the realized reward, not the expected reward.
○ Step 4. Update $Q̂(x, u)$
③ Supplements
○ Learning the full model requires $\left|\mathcal{S}\right|^2\left|\mathcal{A}\right|$ memory, but Q-learning only needs $\left|\mathcal{S}\right|\times\left|\mathcal{A}\right|$ memory.
○ It is also referred to as TD (temporal-difference) learning.
○ Proof on convergence of Q-learning: Pseudo-contraction mapping
⑶ Type 2. SARSA (State-Action-Reward-State-Action; ε-greedy, epsilon greedy) (Rummery & Niranjan, 1994)
① Overview
○ Depends on policy (on-policy).
○ When there is no data available, it chooses a policy and collects new data through interaction with the environment.
② Formula
○ Step 1. Initialize estimates for all state/action pairs: Q̂(s, a) = 0
○ Step 2. At each step $k$, with probability 1 - εk, take u ∈ arg maxv Q̂(x, v); with probability εk, take a random action
○ Step 3. Observe the next state $x’$ and receive $R(x’, u)$: Note that this is the realized reward, not the expected reward.
○ Step 4. Update Q̂(x, a)
○ Step 5. As $k \to \infty$, drive $\varepsilon_k \to 0$; in this case, one can also use a Boltzmann (softmax) distribution with temperature annealing $(T \to 0)$.
③ Comparison with Q-learning
○ Target policy: the policy to be learned
○ Behavior policy: the policy used to generate samples
○ Q-learning: target policy = optimal policy; behavioral policy = any policy under which each action is taken infinitely often
○ SARSA: target policy = ε-greedy policy; behavioral policy = ε-greedy policy
○ Supplement 1. Using an ε-greedy behavior policy doesn’t automatically make it SARSA; what matters is the target policy used in the update.
○ Supplement 2. “Off-policy” means that no matter which policy collected the data, the update uses a greedy target (i.e., the max over next actions).
○ Supplement 3. If the behavior policy is fully greedy (ε = 0), then in SARSA $a’ = \arg\max_{a} Q(s’, a)$, so the targets match and the update equations become essentially the same.
⑷ Type 3. Linear Function Approximation
① Purpose: The memory space of Q-learning is ㅣ𝒮ㅣ × ㅣ𝒜ㅣ, while that of linear function approximation is M ≪ ㅣ𝒮ㅣ × ㅣ𝒜ㅣ.
② Formula: note that δk2 is always non-negative.
⑸ Type 4. DQN (Deep Q-Network)
① Definition: Implementation of Q-learning using deep learning
② Applied to many games: DQN on Atari 2600 (2013), AlphaGo (2016), etc.
⑹ Type 5. Policy Gradient
① Definition: Learning policy π(s) directly
② Characteristics
○ In Q-learning, states can be continuous, but actions must be discrete
○ In policy gradient, both states and actions can be continuous
③ Algorithm
○ Step 1. Receive frame
○ Step 2. Forward propagate to get P(action)
○ Step 3. Sample a from P(action)
○ Step 4. Play the rest of the game
○ Step 5. If the game is won, update in the ∇θ direction
○ Step 6. If the game is lost, update in the -∇θ direction
⑺ Other Types
① Deep O-Network (DON)
② A3C (Asynchronous Advantage Actor-Critic)
③ GA(Genetic Algorithm)
4. General Decision Process
⑴ MAB(multi-armed bandit)
⑵ UCB
Input: 2021.12.13 15:20
Updated: 2024.10.08 22:43