Chapter 15. Analysis of Variance (ANOVA)
Higher category: 【Statistics】 Statistics Overview
1. ANOVA
1. Analysis of Variance (ANOVA)
⑴ definitio n: a statistical analysis comparing n groups (assuming n > 2)
⑵ type Ⅰ error inflation: problems occur when performing t test in n numbers of groups (assuming n > 2)
① probability of 1 group having no type Ⅰ error (significance level 5%) : 0.95
② probability of n numbers of groups having no type Ⅰ error for all (significance level 5%) : 0.95n
③ probability of n numbers of groups having type Ⅰ error at least once (significance level 5%) : 1 - 0.95n ≫ 0.05
④ due to type Ⅰ error inflation, ANOVA is introduced
⑶ assumptions: these are required for one-way ANOVA and two-way ANOVA
① normality
○ definition: all data is extracted from populations that follow a normal distribution
○ types of Normality Tests: Q-Q plot, Shapiro-Wilk test, Kolmogorov-Smirnov test, D’Agostino-Pearson test
○ if populations are difficult to see as a normal distribution, use power transformation or log transformation to make them analogue normal distributions
○ Welch ANOVA F-test doesn’t assume homoscedasticity.
○ here, a few populations are considered because the means of the populations may vary

Figure 1. example of making an analogue normal distribution through log transformation
② independency: also known as i.i.d.
○ definition : every data is extracted independently from the populations
○ related to experimental design
○ here, a few populations are considered because the means of the populations may vary
③ homoscedasticity
○ definition : all data are derived from the populations with the same variance, even though the means of the populations are different
○ if the ratio of the largest and smallest variance does not exceed 4:1, analysis of variance can be used
○ if it is difficult to use ANOVA, use square root transformation to minimize the difference of variances
○ equal variances in regression analysis mean that the variances of Yi are constant for each Xi: slightly different in meaning of homoscedasticity between analysis of variance and regression analysis
○ Welch ANOVA should be applied if the homoscedasticity is not satisfied
⑷ robustness
① definition : a characteristic that statistical conclusions do not change even in heteroscedasticity and non-normality when a large number of samples, the same number of repetitions within a category, etc. are satisfied
② robustness of ANOVA : ANOVA applies comparatively better than others even if its homoscedasticity and normality are not strictly satisfied
③ robustness of regression analysis: a characteristic that adding or changing a regression variable does not significantly change the value of a particular coefficient
⑸ (comparison) regression analysis and cross-analysis
① analysis of variance: independent variables are categorical (classified) variables. dependent variables are measurable variables
② cross analysis: independent variables are categorical (classified) variables. dependent variables are categorical (classified) variables
③ regression analysis: independent variables are measurable variables. dependent variables are measurable variables
2. one-way ANOVA
⑴ definition: a case of ANOVA in which there are only 1 independent variable and 1 dependent variable
① an independent variable is called a treatment effect or Factor
② examples of appropriate dependent variables :{height}, {weight}(O)
③ an example inappropriate dependent variables :{height, weight} (X)
⑵ one-Way ANOVA model
① model 1. fixed effect modeling
○ definition: comparing the effects of certain objects. in other words, levels of Factors are fixed
○ method: trials of extraction from a population are not required. post hoc analysis is important
○ example: control, treatment A, treatment B
② model 2. random effect modeling
○ definition : looking at the general trend of the population. in other words, levels of Factors are random
○ method : samples are randomly extracted from the population and subjected to ANOVA analysis. post hoc analysis is not required
○ example : when the owner of the Factory wants to ensure that the weights of all the Factory products are the same
③ in one-way ANOVA, the fixed effect modeling and the random effect modeling follow the same calculation procedure
⑶ problem situation
| Factor | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| Sample | 11 | 8 | 5 |
| 10 | 7 | 4 | |
| 8 | 5 | 2 | |
| 7 | 4 | 1 | |
| Average | 9 | 6 | 3 |
Table 1. example of one-way ANOVA
① X̄1 = 9, X̄2 = 6, X̄3 = 3, X̄ = 6
② sample sizes for Group 1, Group 2, and Group 3 are allowed to be different
⑷ setting hypotheses
① H0 : μGroup 1 = μGroup 2 = ··· = μGroup m = μ (assuming m = 3 in the above situation)
② H1 : at least a pair of population mean is not equal
⑸ derivation of F statistic
① idea: if the variance within the group is clearly smaller than the variance between groups, it can be said that there is a difference between sample groups
② definition

③ sum of squares (SS)

④ calculation of variance ratio
○ variance ratio: also called F ratio
○ among-group variance: related to error and treatment effect
○ within-group variance: related to error

⑤ table of results
| Factor | Sum of Squared | Degree of Freedom | Mean of Square | F ratio | p value |
|---|---|---|---|---|---|
| Effect | 72 | 2 | 36 | 10.8 | 0.0040583 |
| Error(Residual) | 30 | 9 | 3.33 | ||
| Sum | 102 | 11 |
○ sum of squares of error = among-group variance + within-group variance = 72 + 30 = 102
○ total degree of freedom = degree of freedom of among-group variance + degree of freedom of within-group variance = (k - 1) + (n - k) = n - 1
○ group variable is not a number, so calculating the coefficient of determination is meaningless
○ report example: ”A single-Factor ANOVA showed a significant difference among the three treatments (Group 1, Group 2, and Group 3): F2.9 = 10.8, p < 0.01”
○ Tip. when calculating 72 and 30, 12 terms are used (∵ symmetry)
⑹ proof of F statistic
② distribution of among-group variance

③ distribution of within-group variance
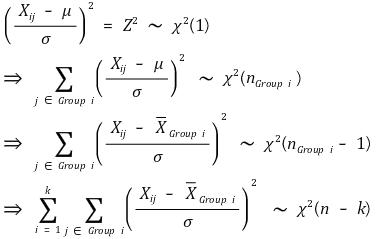
④ distribution of variance ratio

⑺ characteristics
① if the number of samples in each group is similar, the power is high
② if the number of samples in a specific group is small, reliability is suspected
③ rejecting the alternative hypothesis does not always conclude that a pair of means are different in pairwise t testing
④ unlike pairwise t testing, post-hoc analysis (poster analysis) indicates which pair of groups are different
⑻ Levene test: test for heteroscedasticity


Figure 2. an example of Levene test
① 1st. examine the absolute value of each deviation calculated as the difference from the mean of each related sample group
○ control: (8, 7, 7, 8)
○ Tumostat: (2, 1, 1, 2)
○ Inhibin 4: (2, 1, 1, 2)
② 2nd. perform one-way ANOVA on three new groups
③ 3rd. control group clearly shows a large deviation compared to the other two groups: homoscedasticity is rejected
④ Other test for heteroscedasticity: Bartlett’s test
⑼ post hoc analysis: basically, it is derived from multiple comparison
① LSD, Bonferroni, Sidak, Tukey, Duncan, Dunnett, Scheffe, Student-Newman-Keuls, BH procedure, etc
○ Scheffe, Tukey, Duncan, and Student-Newman-Keuls are most popular
○ of the three, Scheffe is the most conservative and Duncan is the most loose
○ in nature science: generlly, Tukey is tested at first and Duncan is used if Tukey test is not significant
○ in social science: generally, Scheffe is used frequently
② example : Tukey HSD (Honestly significant difference, Tukey-Kramer method)
○ Different from Bland-Altman test.
○ statistics

○ test


Figure 3. multiple comparison test after ANOVA
○ situation 1. A > B > C > D > E in sample mean
○ situation 2. as a result of one-way ANOVA, all means are not equal
○ 1st. test with Tukey statistics in an order of A-E, A-D, A-C, and A-B: the A-C is not significant, so the A-B test is omitted
○ 2nd. test with Tukey statistics in an order of B-E, B-D, and B-C : the A-C is not significant, so the B-C test is omitted
○ 3rd. test with Tukey statistics in an order of C-E and C-D
○ 4th. test D-E with Tukey statistic
○ if not sorted by size, a total of 10 tests will make 10 times of type Ⅰ error, i.e. type Ⅰ error inflation
○ in the above case, the situation is a slightly better because there appears only 8 times of the type Ⅰ error
③ cautions in post hoc analysis
○ example
| Control | Neurohib | Mitostep |
|---|---|---|
| 7 | 4 | 1 |
| 8 | 5 | 2 |
| 10 | 7 | 4 |
| 11 | 8 | 5 |
Table 3. example of post hoc analysis
○ result

Figure 4. cautions in post hoc analysis
○ the reason why Control = Neurohib and Neurohib = Mitostop, but Control ≠ Mitostop is type Ⅰ error
○ example : if the probability of A = B is 10% and B = C is 10% then the probability of A = B = C is 1%, which is significantly different
3. two-way ANOVA
⑴ overview
① definition : attempting to an analysis of variance for two independent variables, one dependent variable
② not only the main effect of each Factor but also their interaction is of interest
③ assumptions
○ normality : populations follow the normal distribution
○ independency : samples are randomly extracted from populations
○ homoscedasticity : populations have the same variance
○ orthogonality : two Factors are not correlated with each other
○ Satisfaction with orthogonality has nothing to do with no interaction: Understanding the differences in concepts is necessary.
⑵ classification of situation

Figure 5. classification of experiment results for Two Factors
⒜ no temperature effect; no humidity effect
⒝ no temperature effect; existent humidity effect
⒞ existent temperature effect; no humidity effect
⒟ existent temperature effect; existent humidity effect
⒠ existent temperature effect; existent humidity effect; existent interaction
⑶ two-way ANOVA Model
① reasons why random effects should be calculated differently in a two-way analysis of variance

Figure 6. the reasons why random effects should be calculated differently in a two-way analysis of variance
○ situation : B2 and B4 are randomly extracted levels from Factor B
○ expectation : the main effect of A should be ambiguous
○ reality: the main effect of A seems to be existent due to the random sampling effect
② model 1. fixed effect modeling: the levels of the two Factors are fixed
| Factor | Sum of Squared | Degree of Freedom | Mean of Square | F ratio |
|---|---|---|---|---|
| A | SSA | dfA = I-1 | MSA = SSA ÷ dfA | FA = MSA ÷ MSE |
| B | SSB | dfB = J-1 | MSB = SSB ÷ dfB | FB = MSB ÷ MSE |
| A × B | SSA×B | dfA×B = (I-1)(J-1) | MSA×B = SSA×B ÷ dfA×B | FA×B = MSA×B ÷ MSE |
| Error(Residual) | SSE | dfE = n-IJ | MSE = SSE ÷ dfE | |
| Sum | SST | n-1 |
Table 4. table of results of fixed effect modeling
③ model 2. random effect modeling: the levels of two Factors are random
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-ratio |
|---|---|---|---|---|
| A | SS_A | df_A = I - 1 | MS_A = SS_A ÷ df_A | F_A = MS_A ÷ MS_A×B |
| B | SS_B | df_B = J - 1 | MS_B = SS_B ÷ df_B | F_B = MS_B ÷ MS_A×B |
| A × B | SS_A×B | df_A×B = (I - 1)(J - 1) | MS_A×B = SS_A×B ÷ df_A×B | F_A×B = MS_A×B ÷ MS_E |
| Error (Residual) | SS_E | df_E = n - IJ | MS_E = SS_E ÷ df_E | |
| Total | SS_T | n - 1 |
Table 5. table of results of random effect modeling
④ model 3. mixed effect modeling: one Factor has a fixed level and the other Factor has a random level
| Factor | Sum of Square | Degree of Freedom | Mean of Square | F 비 |
|---|---|---|---|---|
| A | SSA | dfA = I-1 | MSA = SSA ÷ dfA | FA = MSA ÷ MSA×B |
| B | SSB | dfB = J-1 | MSB = SSB ÷ dfB | FB = MSB ÷ MSE |
| A × B | SSA×B | dfA×B = (I-1)(J-1) | MSA×B = SSA×B ÷ dfA×B | FA×B = MSA×B ÷ MSE |
| Error(Residual) | SSE | dfE = n-IJ | MSE = SSE ÷ dfE | |
| Sum | SST | n-1 |
Table 6. table of results of mixed effect modeling
○ A is a fixed effect and B is a random effect
○ tip. understand by comparing it with the below nested analysis of variance
⑷ example : fixed effect modeling
| Humidity (%) | Temperature (℃) | ||
|---|---|---|---|
| 20 | 30 | 40 | |
| 33 | 1 | 5 | 9 |
| 2 | 6 | 10 | |
| 3 | 7 | 11 | |
| 66 | 9 | 13 | 17 |
| 10 | 14 | 18 | |
| 11 | 15 | 19 | |
| 99 | 17 | 21 | 25 |
| 18 | 22 | 26 | |
| 19 | 23 | 27 |
Table. 7. example of two-way ANOVA

① definition

② sum of squares

③ calculation of variance ratio

④ table of results
| Factor | Sum of Square | Degree of Freedom | Mean of Square | F ratio | p value |
|---|---|---|---|---|---|
| Temperature | 288 | 2 | 144 | 144 | 8.43e-12 |
| Humidity | 1152 | 2 | 576 | 576 | < 2e-16 |
| Temperature × Humidity | 0 | 4 | 0 | 0 | 1 |
| Error(Residual) | 18 | 18 | 1 | ||
| Sum | 1464 | 26 |
Table 8. table of results
○ null hypothesis 1. μ20℃ = μ30℃ = μ40℃ = μ : this null hypothesis is rejected because p value = 8.43e-12 < 0.05
○ null hypothesis 2. μ33% = μ66% = μ99% = μ : this null hypothesis is rejected because p value < 2e-16 < 0.05
○ null hypothesis 3. interaction of temperature and humidity = 0: this null hypothesis is not rejected because p value = 1
○ coefficient of determination = 1 - 18 ÷ 1464 = 0.987704918
○ correlation coefficient = ± √ 0.987704918 = 0.993833445
○ the sign of the correlation coefficient is determined in accordance with the sign of the estimator for the slope
⑤ the interaction obscures the main effect, so you should not believe the F value when there is a significant interaction
○ for example, if substance A promotes gene expression and substance B inhibits gene expression,
○ when substance A and substance B are treated at the same time, there is no significant change in gene expression
○ though, both A and B are not ineffective.
⑸ application 1. test without replication
① overview
○ not possible in one-way ANOVA
○ used when the number of experimental populations is insufficient or expensive
② example
| Radiation Level | Drug | Average | ||
|---|---|---|---|---|
| Proshib | Testosblock | Control | ||
| Low | 81 | 76 | 79 | 78.67 |
| Medium | 45 | 46 | 45 | 45.33 |
| High | 28 | 27 | 27 | 27.33 |
| Average | 51.33 | 49.67 | 50.33 | 50.44 |
Table 9. example of test without replication
③ table of results
| Factor | Sum of Square | Degree of Freedom | Mean of Square | F ratio | p value |
|---|---|---|---|---|---|
| Drug | 4070.222 | 2 | 2035.111 | 832.546 | 5.74e-06 |
| Radiation | 4.222 | 2 | 2.111 | 0.864 | 0.488 |
| Error(Residual) | 9.778 | 4 | 2.444 | ||
| Sum | 4084.222 | 8 |
Table 10. table of ANOVA results of test without replication
○ ANOVA of test without replication should never include an interaction term
○ if you include an interaction term, the degree of freedom of residuals of the term = (RC - 1) - (R - 1 + C - 1 + (R - 1)(C - 1) = 0, so the F ratio cannot be calculated
⑹ application 2. randomized block experimental design: an example of non-repeating analysis of variance
① definition : after dividing the region into several blocks, each block is subdivided again to experiment with different Factors

Figure 7. randomized block experimental design
○ two-way ANOVA is possible: there are two Factors; regional specific Factor of a block and treatment Factor
○ objective: to increase the reliability of the statistical conclusion of the treatment by separating regional specific Factor
② process
○ 1st. divide the entire region into several regions
○ 2nd. randomly assign block numbers to each region
○ 3rd. each block is divided into sub-blocks as many as the number of levels of the treatment
○ 4th. randomly assigns the location of the level of the treatment on each sub-block
○ 5th. repeat measurements for each treatment in each block
○ 6th. a statistically significant block Factor indicates that a region-specific Factor is clearly present
○ region-specific Factor: presence of groundwater, difference in daylight, presence of underground lode, etc
③ result

Table 11. a result of randomized block experimental design
⑺ application 3. nested analysis of variance
① analogue two-way analysis : in reality, it is classified as one-way ANOVA
② example
○ problem situation
| Prawn Food + Vitamin A | Prawn Food | ||
|---|---|---|---|
| Pond 1 | Pond 2 | Pond 3 | Pond 4 |
| 30 | 60 | 80 | 110 |
| 35 | 65 | 85 | 115 |
| 45 | 75 | 95 | 125 |
| 50 | 80 | 100 | 130 |
Table 12. a situation of nested analysis of variance

Figure 8. a situation of nested analysis of variance
○ calculation of F statistic
| Factor | Sum of Square | Degree of Freedom | Mean of Square | F ratio | p value |
|---|---|---|---|---|---|
| Diet | 10000.0 | 1 | 10000.0 | 5.556 | 0.143 |
| Pond(Diet) | 3600.0 | 2 | 1800.0 | 21.600 | 0.000 |
| Error(Residual) | 1000.0 | 12 | 83.3 | ||
| Sum | 14600.0 | 14 |
Table 13. calculation of F statistic in nested analysis of variance
○ actual calculation: when calculating 10000, 3600, and 1000, the number of terms on the right side is 16 (∵ symmetry)

③ similar to a randomized block experimental design, but clear differences exist
○ difference 1. Pond 1, Pond 2, Pond 3, and Pond 4 cannot be classified into any block
○ difference 2. not satisfied with orthogonality, which is basically the assumption of two-way ANOVA: Diet and Pond(Diet) are not orthogonal
○ difference 3. difference in the calculation of the degree of freedom calculation: the degree of freedom of Pond (Diet) is 2 in total, with Pond 1 ↔ Pond 2 and Pond 3 ↔ Pond 4
○ in the example above, if you are designing a randomized block experimental design, the degree of freedom for the block is 1
○ the randomized block experimental design increases the degree of freedom of error, thus increasing the F ratio (increasing the power of the test)

○ the reason why we aim to design a randomized block experimental design rather than nested analysis of variance
○ difference 4. calculate like Pond × Diet without seeing Pond as an independent Factor
Input : 2019.11.16 17:36