Chapter 12. Error Analysis
Higher category: 【Statistics】 Statistics Overview
3. significant figure of measured values
1. essence of error
⑴ measure: determination of measured values in strictly defined units
⑵ error = measured Value - true value
⑶ the uncertainty principle of quantum mechanics makes it impossible to know the true value of any measurement
⑷ since the true value is not accurate, it is reasonable that the error is considered to be a specific range rather than a specific value. related to probability error
2. types of error
⑴ unfair error
① definition : errors that occur when a measurement is unreliable due to an apparent error in instrument operation
② example 1. if one origin is not set when measuring length
③ example 2. if the resistance measurement does not confirm the origin
④ solution: since the cause is obvious, we should neglect the data
○ if these are included, the reliability of other measurements is poor.
⑵ systematic error
① definition: error due to unstable measuring instrument.
② characteristic: it can estimate the size and sign and correct the error
③ example 1. the case in which the average value was obtained by measuring the voltage several times, and as a result of checking, the scale of the voltmeter used deviated from its origin
④ example 2. the case in which the length was measured with a ruler, but the change in length with temperature was not considered
⑤ example 3. truncation error: error caused by taking only a specific term from a solution expressed in series (e.g., Taylor series)
⑶ random error
① definition : an error due to fluctuations in measurements that result from different results of repeated measurements
② solution : use a more precise measuring instrument or repeat several times
③ reducing random error is the most important factor in improving experimental results
⑷ probable error
① definition: the size of error assumed when acquiring measured value
② it’s not the cause of the error, but how to express it
③ it is represented by σp and used in a way of “measured value x = xavg ± σp“
○ it doesn’t mean that the error of x is σp
○ it means that the probability of x deviating more than ±σp is small
○ set σp so that the probability that the true value is between xavg - σp and xavg + σp is 50%
④ errors are normally distributed, and if the standard deviation of the error is σm, the probability that the true value is between xavg - σm and xavg + σm is approximately 68 %
⑤ if we set σp = 0.67 σm, the probability that true value is between xavg - σp and xavg + σp is 50%
3. significant figure of measured values
⑴ necessity : all measurements are approximated, so the measurements should only show valid numbers, i.e. only significant figure
⑵ rules for significant figure selection
① the leftmost number other than 0 is the highest significant figure
② if there is no decimal point, the rightmost number other than 0 is the lowest significant figure
③ if you have a decimal point, even if the number on the far right is 0, this number is the lowest significant figure
④ all numbers between the highest and lowest significant figures are also significant figures
⑤ example: only the underlined part is the significant figure
○ 994.29
○ 56000
○ 0.0048
○ 6.000
○ 800.
○ 2.990 × 104
⑶ rules for significant figure calculation: reducing waste of unnecessary calculation time when calculating measurements
① addition and subtraction: if we calculate the summation of 7.9 and 0.1637,
○ the number 7.9 has no significant number at two decimal places, so 0.1637 is cut there → 0.16
○ 7.9 + 0.16 = 8.06
○ if you round it up to one decimal place, 8.06 → 8.1
② multiplication and division: if you calculate the product of 7.9 and 0.1637,
○ 7.9 × 0.1637 = 1.29323
○ 7.9 has two significant figures and 0.1637 has four significant figures, so you can round the results to two digits
○ 1.29323 → 1.3
4. standard error
⑴ necessity : measured values have some distribution due to random error → a number that can represent them is required
⑵ type 1. mode : the most frequently measured value
⑶ type 2. median : measurements placed in the center when the data are listed in order of size
⑷ type 3. average (mean): the arithmetic mean of the measured values
① when the N measurements are said x1, x2, ···, and xN,
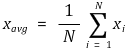
② if the frequencies of each measured value x1, x2, ···, and xN are f1, f2, ···, and fN respectively,
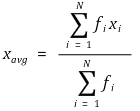
③ calculation of variance σ2

④ if the physical quantity per round is measured M times, the average value and standard deviation of the measured values obtained each round are different
⑤ if the standard deviation of the sample mean xavg is σm, the following relationship is established between σ, σm, and N
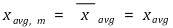
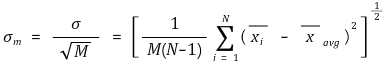
○ σm is also referred to as standard error
⑥ the measurements to be reported from the measurement data are as follows.
x = xavg ± σm
⑦ in general physics experiments, it is common to report a measurement using a probability error that sets the confidence coefficient to 50%
x = xavg ± σp = xavg ± 0.6745σm
⑧ how to depict an error
○ absolute error: report in the form of σ
○ relative error: report in the form of σ / |xavg|
○ percent error: report in the form of σ / |xavg| × 100
5. propagation of error
⑴ example: an experiment to find out the volume of a cube
① method 1. obtaining data on 1,000 volumes and calculating the mean value and standard deviation
② method 2. calculating the volume by multiplying each average value for width, length, and height first and multiplying these average values
③ method 2 is much more convenient, but errors are accumulated.
⑵ propagation theory of errors
① assume that a physical quantity z is given as a relation of another physical quantity x, y, ··· in a way of z = f(x, y, ···)
② assume that the mean values (sample mean) of xavg, yavg, ··· and the standard deviation σx, σy, σz were obtained from the measurements of x, y, ···
③ mean of the z, i.e. zavg
zavg = f(x= f(xavg, y, yavg, ···), ···)
④ standard deviation of z, i.e. σz

⑤ (∂f/∂x)0, ,(∂f/∂y)0, ··· means partial derivatives calculated from the average values of xavg, yavg, ···
⑶ propagation formula of errors
① z = ax ± by

② z = axy
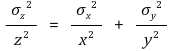
③ z = ax/y
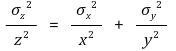
④ z = axb
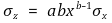
⑤ z = aebx
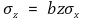
⑥ z = a log(bx)
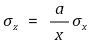
⑷ suggestion
① rules for significant figure calculation stem from the propagation formula of errors.
② in the case of the power function, the larger the exponent, the larger the propagating error, so a particularly precise measurement is required
6. least square method
⑴ most probable value: representative value that minimizes the sum of the squares of the deviation.
⑵ least square method
① assume that x1, x2, ···, xN are obtained from the repetitive measurements of an amount
② if the most probable value is x, the sum of the squares of the deviation is as follows
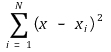
③ this is considered a function of x, and the condition under which this function has a minimum value is as follows
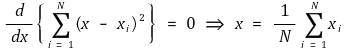
④ in this particular condition, the mose probable value is the same with the mean value
⑶ it’s often used to find polynomial trend lines
Input : 2019.04.13 01:28