Shortest Path Algorithm in C Language (Floyd algorithm)
Higher cateogyr : [C Language] C Language Table of Contents
2. Example 1: Shortest path algorithm using Bellman equation
3. Example 2: Dijkstra algorithm
4. Example 3: Shortest path algorithm implemented in C language
a. GitHub
1. (Reference) Various distance concepts
⑴ Distance function: Defines the distance
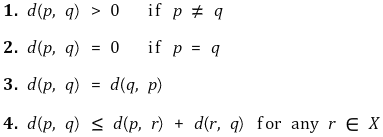
⑵ Type 1: L1 distance
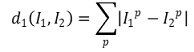
⑶ Type 2: L2 distance: Euclidean distance using the Pythagorean theorem (Standard)
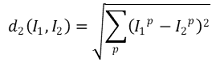
⑷ Type 3: p-norm
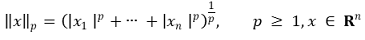
⑸ Type 4: dot product
⑹ Type 5: linkage metric: Defines the distance between clusters
⑺ Type 6: [KL distance](https://jb243.github.io/pages/2145#:~:text=%E2%91%A7-,%EC%83%81%EB%8C%80%20%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC,-(relative%20entropy%2C)(Kullback-Leibler divergence)
⑻ Type 7: Hamming distance: Measures the distance between data points by specifying binary values for each of them
⑼ Type 8: Mahalanobis distance: Measures the distribution of data
2. Example 1: Shortest path algorithm using Bellman equation
Consider a rooted binary tree network. Each internal node x has two children, denoted by x(lhs) and x(rhs). The cost of moving from x to its child x(a) is la, where a ∈ {lhs,rhs}. For each node x, let Lx be the minimum cost of any path from x to a leaf node. For each leaf node y, define Ly = 0. Show that for any internal node x the following holds:
The proof can be found in this link.
3. Example 2: Dijkstra algorithm
⑴ Problem: The following figure shows a directed weighted graph with vertex set (V={A,B,C,D,E,F,G,H}). Using Dijkstra’s algorithm, find the shortest distance and shortest path from vertex A to vertex H.
⑵ Solution
① Initialization
○ d[A]=0, and all other d[·] = ∞
② Start from A and relax adjacent vertices
○ d[B] = 7, d[D] = 8, d[C] = 12
③ Among unvisited vertices, the current minimum is B (7) → relax from B
○ (d[D] = min(current d[D], d[B] + 5) = current d[D] = 8) → no improvement
○ d[E] = min(current d[E], d[B] + 9) = d[B] + 9 = 16 → updated to 16
④ Among unvisited vertices, the current minimum is D (8) → relax from D
○ d[E] = min(current d[E], d[D] + 2) = d[D] + 2 = 10 → updated to 10
○ d[G] = min(current d[G], d[D] + 14) = d[D] + 14 = 22 → updated to 22
○ d[C] = min(current d[C], d[D] + 5) = current d[C] = 12 → no improvement
⑤ Among unvisited vertices, the current minimum is E (10) → relax from E
○ d[H] = min(current d[H], d[E] + 3) = d[E] + 3 = 13 → updated to 13
⑥ Among unvisited vertices, the current minimum is C (12), but (d[H]) is not improved
⑦ Among unvisited vertices, the current minimum is the target vertex H, so (d[H]) is finalized → stop
⑧ Conclusion
○ Shortest distance: 13
○ Shortest path: A → D → E → H
4. Shortest path algorithm implemented in C language
⑴ Problem situation: For example, the path from 0 to 5 requires a cost of 6. In other words, it requires moving a distance of 6.
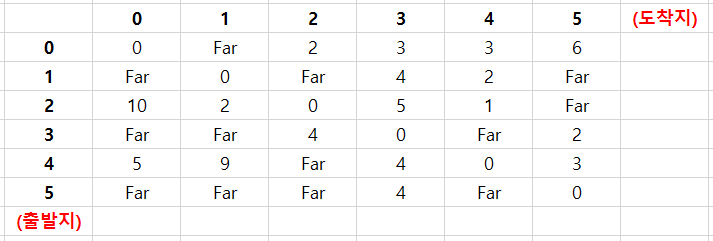
Table 1. Problem situation
⑵ Dijkstra algorithm: Characterized by two-nested for phrase
#include <stdio.h>
#include <stdlib.h>
#define Count_Vertice 6
#define Far_Distance 2000
// W[i][j] indicates the direct distance from i to j, and Far_Distance indicates that it cannot go directly
int W[Count_Vertice][Count_Vertice] = {
{0, Far_Distance, 2, 3, 3, 6},
{Far_Distance, 0, Far_Distance, 4, 2, Far_Distance},
{10, 2, 0, 5, 1, Far_Distance},
{Far_Distance, Far_Distance, 4, 0, Far_Distance, 2},
{5, 9, Far_Distance, 4, 0, 3},
{Far_Distance, Far_Distance, Far_Distance, 4, Far_Distance, 0},
};
// dist[i] : the shortest distance from the starting point to i
// prev[i] : the immediately preceding vertex of i in the shortest path from the starting point to i
int dist[Count_Vertice];
int prev_v[Count_Vertice];
int visited[Count_Vertice];
void Dijkstra(int start) {
int i, j;
// 초기화
for (i = 0; i < Count_Vertice; i++) {
dist[i] = W[start][i]; // direct distance from the starting point (if without, it is Far_Distancec)
if (W[start][i] < Far_Distance && i != start)
prev_v[i] = start; // if you can go directly, then start is the preceding vertex.
else
prev_v[i] = -1; // no path
visited[i] = 0;
}
dist[start] = 0;
prev_v[start] = -1; // the starting vertex has no preceding vertex.
// repeat by the number of vertices
for (i = 0; i < Count_Vertice; i++) {
int u = -1;
int min_dist = Far_Distance + 1;
// select the vertex u with the smallest dist among the non-visited vertices
for (j = 0; j < Count_Vertice; j++) {
if (!visited[j] && dist[j] < min_dist) {
min_dist = dist[j];
u = j;
}
}
// shut down if there are no more nodes to go to
if (u == -1) break;
visited[u] = 1;
// attempt to update to route via u
for (j = 0; j < Count_Vertice; j++) {
if (!visited[j] && W[u][j] < Far_Distance) { // if there is an edge of u -> j
if (dist[j] > dist[u] + W[u][j]) {
dist[j] = dist[u] + W[u][j];
prev_v[j] = u;
}
}
}
}
}
// recursively output the route from start point a to destination point b
void Print_Path(int a, int b) {
if (a == b) {
printf("%d ", a);
} else if (prev_v[b] == -1) {
// when there's no path
printf("(No Path) ");
} else {
// print the vertex immediately preceding b first, and then print b.
Print_Path(a, prev_v[b]);
printf("%d ", b);
}
}
int main(void) {
int a, b;
printf("Please enter your starting point and arrival point. (0 ~ %d)\n", Count_Vertice - 1);
if (scanf("%d %d", &a, &b) != 2) {
printf("Input error\n");
return 1;
}
if (a < 0 || a >= Count_Vertice || b < 0 || b >= Count_Vertice) {
printf("Out of range of vertex number.\n");
return 1;
}
// execute dijkstra with a as a starting point
Dijkstra(a);
if (dist[b] >= Far_Distance) {
// unreachable
printf("No path from vertex %d to vertex %d.\n", a, b);
} else {
printf("Shortest distance : %d\n", dist[b]);
printf("Shortest path : ");
Print_Path(a, b);
printf("\n");
}
return 0;
}
⑶ Floyd algorithm(Floyd–Warshall) : Characterized by a triple nested for-loop. More intuitive than Dijkstra’s algorithm.
#include <stdio.h>
#include <stdlib.h>
#define Count_Vertice 6
#define Far_Distance 2000
int W[Count_Vertice][Count_Vertice] = {
// W[i][j] is a direct distance from i to j, and Far_distance is a large number of cases where you can't go right away
{0, Far_Distance, 2, 3, 3, 6},
{Far_Distance, 0, Far_Distance, 4, 2, Far_Distance},
{10, 2, 0, 5, 1, Far_Distance},
{Far_Distance, Far_Distance, 4, 0, Far_Distance, 2},
{5, 9, Far_Distance, 4, 0, 3},
{Far_Distance, Far_Distance, Far_Distance, 4, Far_Distance, 0},
};
int D[Count_Vertice][Count_Vertice]; // D[i][j] stores the minimum distance from i to j
int P[Count_Vertice][Count_Vertice]; // P[i][j] stores the highest order vertex that goes from i to j
void Floyd(){
int i, j, k;
for(i=0; i < Count_Vertice; i++) // array initialization
for(j=0; j < Count_Vertice; j++){
P[i][j] = -1;
D[i][j] = W[i][j];
}
for(k=0; k < Count_Vertice; k++)
for(i=0; i < Count_Vertice; i++)
for(j=0; j < Count_Vertice; j++)
if(D[i][j] > D[i][k] + D[k][j]){
/* D[i][j] becomes shorter when k is passed */
D[i][j] = D[i][k] + D[k][j];
P[i][j] = k;
}
}
void Print_Path(int a, int b){ // note that i and j are not output in Print_Path[i][j]
if(P[a][b] != -1) { // P[a][b] = -1 "=" going directly from **a** to **b** is the shortest path.
Print_Path(a, P[a][b]);
printf("%d ", P[a][b]);
Print_Path(P[a][b], b);
}
}
int main(int argc, char *argv[]){
Floyd();
int a, b;
printf("Please enter your starting point and arrival point. (0 ~ %d)\n", Count_Vertice - 1);
scanf("%d %d", &a, &b);
printf("Shortest distance : %d\n", D[a][b]);
printf("Shortest path : ");
printf("%d ", a); Print_Path(a, b);
if(D[a][b] != 0) printf("%d", b); // D[a][b] = 0 "=" a = b
return 0;
}
Input: December 13, 2013, 22:55