Chapter 8. Clustering Algorithms
Recommended Article: 【Algorithm】 Algorithm Index
1. Introduction
2. Type 1. unsupervised hierarchical clustering
3. Type 2. K-means clustering
4. Type 3. Density-based clustering
5. Type 4. Mixture distribution clustering
6. Type 5. Graph-based clustering
7. Other Clustering Algorithms
1. Introduction
⑴ Clustering is an optimization problem
① variability
○ variability can be defined as the sum of distance or distance squared
○ Reason: big and bad is worse than small and bad
② dissimilarity
○ Clustering is not about finding a global minimum for dissimilarity
○ Reason 1. A trivial solution exists where ∀variability = 0 with as many clusters as samples
○ Reason 2. It’s unfair to penalize large clusters per se: big is not necessarily worse than small
○ Constraints are needed: minimum distance between clusters, number of clusters, etc.
⑵ Clustering is an unsupervised algorithm
① Due to this, evaluating the performance of clustering algorithms is difficult, but it can be assessed as follows
② Clustering Quality Metrics
○ Method 1: Average Silhouette Width (ASW)
○ Formula
○ a(i): The average distance from i to all data points in the same cluster ci
○ b(i): The lowest average distance from i to all data points in the other cluster c among all clusters c.
○ The silhouette coefficient S(c) of cluster c is the average of s(i) for the data points within that cluster.
○ Ranges between -1 and 1.
○ A higher value indicates better clustering quality, meaning higher cohesion within clusters and better separation between clusters.
○ Disadvantages:
○ The score is inversely proportional to the number of clusters.
○ It is inaccurate for non-spherical clusters.
○ Code:
sklearn.metrics.silhouette_score
○ Method 2: Davies-Bouldin Index (DBI)
○ Calculation Process:
○ Measure the similarity between each cluster and the most similar other cluster.
○ Define similarity as the ratio of inter-cluster distance to intra-cluster distance.
○ Average these similarities across all clusters to derive the DBI.
○ The value is 0 or higher; a lower index indicates better cluster separation.
○ Advantages:
○ Less affected by the number of clusters.
○ Disadvantages:
○ May become inaccurate if clusters are poorly separated or if distances vary significantly.
○ Method 3: Calinski-Harabasz Index (CHI)
○ Formula: Relates the number of clusters k and the number of data points n.
○ The value is 0 or higher; a higher value indicates better clustering quality.
○ Disadvantages:
○ The index decreases as cluster sizes increase.
○ Assumes variances are relatively consistent.
○ Method 4: Landscape Shape Index (LSI)
○ Method 5: Percentage of Abnormal Spots (PAS)
○ Higher value indicates lower quality: the proportion of spots considered abnormal (i.e., not consistent with their neighboring spots) among all spots.
○ Used in spatial transcriptomics analysis.
○ Method 6: VoR(variance of the Riemannian metric)
○ A value of 0 indicates a globally uniform space.
○ Method 7: CN(condition number)
○ After SVD, it is the ratio of the largest to the smallest singular value, κ = σmax / σmin.
○ A larger value means the model is more unstable (more ill-conditioned).
② Clustering Comparison Metrics
○ Method 1: Normalized Mutual Information (NMI)
○ Measures mutual information between two clusters and normalizes it to remain invariant to the cluster size or number of classes.
○ Ranges between 0 and 1.
○ Method 2: Adjusted Rand Index (ARI)
○ Evaluates the similarity between two clusters.
○ Ranges between -1 and 1 (perfect match). A score of 0 indicates random clustering.
○ Rand Index (RI)
○ Adjusted for the expected value of random cluster results.
○ Similarly, regarding nij, ai, and bj from the contingency table,
○ Method 3: Adjusted Mutual Information (AMI)
○ Adjusts NMI for the expected value of random clustering.
○ Ranges between -1 and 1.
○ Effective in removing random clustering bias when there are many classes or imbalanced data.
○ Method 4: Fowlkes-Mallows Index (FMI)
○ The geometric mean of precision and recall.
○ Ranges between 0 and 1.
○ Performance decreases with imbalanced data.
○ Method 5: Homogeneity
○ Measures the extent to which samples with the same label are grouped into a single cluster.
○ Method 6: Completeness
○ Evaluates how well samples within the same cluster belong to the same label.
○ Method 7: V-measure
○ Defined as: v = (1 + beta) × homogeneity × completeness / (beta × homogeneity + completeness)
○ Ranges between 0 and 1.
○ Code:
sklearn.metrics.v_measure_score
⑶ Types of Clustering
① Type 1. Hierarchical algorithm: Successively splits or merges groups based on some distance measurement.
○ A deterministic approach.
○ 1-1. Agglomerative: bottom-up approach. An approach that builds larger clusters.
○ 1-2. divisive: top-down approach. An approach that divides into smaller clusters. Most common implementation.
② Type 2. Partitioning algorithm: Looks for a specific delineation that optimizes some global measure
○ 2-1. Hard
○ 2-2. Soft
⑷ Clustering Alignment Algorithm
① Challenges of clustering alignment: label switching, multi-modality, different K value
② Example 1. Gale–Shapley (Stable Matching)
○ Problem: Two sets (e.g., men/women, students/schools) each have preference rankings over the other side.
○ Goal: Find a stable matching—one with no blocking pair (i.e., no two participants who would both prefer each other over their current matches).
○ Key feature: The focus is stability, not cost minimization. The outcome is optimal for the proposing side (proposer-optimal stable matching).
③ Example 2. Hungarian assignment algorithm
○ Problem: An assignment/bipartite matching setting where each possible pair has a cost (weight).
○ Goal: Find an optimal matching that minimizes total cost (or equivalently maximizes total profit/benefit).
○ Key feature: The focus is optimization, not stability; it does not use the stable-matching notion.
○ Principle: As illustrated in the schematic below, it iteratively minimizes the costs of components that contribute to one-to-one matching and, conversely, maximizes the costs of components that hinder such matching, thereby finding the optimal one-to-one correspondence.
Figure 1. Hungarian assignment algorithm
2. Type 1. Unsupervised hierarchical clustering
⑴ Overview
① Often used to draw a heatmap from an internal matrix (Example: RStudio’s heatmap function)
② A type of graph-based method
③ Unlike non-hierarchical clustering, hierarchical clustering does not pre-determine the number of clusters
⑵ Type 1. Divisive Analysis
① A technique that starts from the entire group and separates objects with decreasing similarity
② Stage 1: Initially assign N elements to N clusters
③ Stage 2: Merge the closest clusters into one
④ Stage 3: Repeat stage 2 until constraints such as the number of clusters are met
○ In this case, a dendrogram is used
⑶ Type 2. Agglomerative Hierarchical Clustering
① Definition: A method that considers each entity as a subgroup and progressively merges similar subgroups to form new subgroups
② Example 1. UPGMA(unweighted pair group method with arithmetic mean)
⑷ Linkage metric: Defining distance between clusters
① Type 1. Single-linkage: The shortest distance between elements of one cluster and another
② Type 2. Complete-linkage: The farthest distance between elements of one cluster and another
③ Type 3. Average-linkage: The distance between the centers of two clusters
○ Can also mean the average distance between elements of one cluster and another
④ Type 4. Centroid-linkage: Measuring the distance between the centers of two clusters
⑤ Type 5. Ward-linkage: A method of measuring distance between clusters based on within-cluster sum of squares
Figure 2. Performance of clustering according to linkage metric
⑸ Features
① One of the most frequently used clustering algorithms along with K-means clustering
② Advantage 1. Deterministic: can reach the same conclusion in any environment
③ Advantage 2. Can try various linkage criteria
④ Disadvantage 1. Slow naïve algorithm. Generally requires Ο(n3) time complexity
○ Reason: Ο(n2) is required to perform stage 2 and it has to be repeated Ο(n) times
○ In some cases, Ο(n2) time complexity is required depending on the linkage criteria
3. Type 2. K-means clustering
⑴ Overview
① Often used in clustering algorithms targeting images
⑵ Algorithm
Figure 3. How K-means clustering works
① Stage 1: Randomly select k initial centroids
② Stage 2: Assign clusters based on which centroid each element is closest to
③ Stage 3: Calculate the center of each cluster to define new centroids
④ Stage 4: Clustering ends when centroids no longer change
⑶ Features
① The most widely used clustering algorithm
② K-means clustering is one of the greedy algorithms for clustering
③ Determining K
○ Background knowledge
○ Example: Differentiating between cancerous and non-cancerous data in bio multi-omics data
○ Elbow Method
○ A method to determine the number of clusters in cluster analysis by plotting the total within-cluster sum of squares against the number of clusters and selecting the elbow point as the appropriate number of clusters
○ Choose the cluster corresponding to the elbow part where the slope is gentle when the number of clusters is on the x-axis and SSE value on the y-axis
○ Silhouette Method
○ A method that quantitatively calculates the quality of clustering using silhouette coefficients
○ Shows how well clusters are separated from each other
○ A silhouette coefficient close to 1 indicates well-optimized, well-separated clusters
○ A silhouette coefficient close to 0 indicates poorly optimized, closely spaced clusters
○ Dendrogram
○ Use dendrogram visualization in hierarchical cluster analysis to determine the number of clusters
④ Advantage
○ Advantage 1. Fast. Ο(Kn) time is required to perform stage 2 (K is the number of clusters, n is the number of data points)
○ Advantage 2. Mathematically converges after a finite number of iterations as the objective function decreases with each iteration
○ Advantage 3. Algorithms are relatively simple
○ Advantage 4. A tool of Data Mining
⑤ Disadvantage
○ Disadvantage 1. K should be given: Choosing the wrong K can lead to incorrect results
○ Disadvantage 2. Depends on initial centroids: Results can vary depending on initial centroid position, so it’s not deterministic
○ Disadvantage 3. The complex data cannot be clustered because it relies on the Euclidean distance for specific points.
○ Each feature that makes up the data needs to be bi-modal or multi-modal for it to work well. (ref)
○ Example 1: When the data consists of two concentric circles, the positions of the two centroids are the same, so K-means clustering cannot be used.
○ Example 2: When the clusters are not spherical.
Figure 4. When the clusters are not spherical
○ Example 3: When the clusters have different densities.
Figure 5. When the clusters have different densities
⑥ Overcoming
○ ISODATA: Estimates the value of K
○ Kohonen Self-Organizing Map: Similar to evolutionary learning, gradually increases the value of K to reduce variability
○ K-medoid clustering
○ Lloyd’s K-means clustering algorithm
○ Bisecting K-Means: Provided by scikit package
○ Fuzzy c-means clustering: Points belong to more than one cluster.
○ Mean-shif: Provided by scikit package. Points are moved to the densest nearby area.
⑷ Python code
from sklearn.cluster import KMeans
X = [[1, 2, 3],[1, 2, 3.1],[2, 2, 4],[2, 2, 4.1]]
kmeans = KMeans(n_clusters=2, random_state=0)
kmeans.fit(X)
cluster_labels = kmeans.labels_
print(cluster_labels)
# [1 1 0 0]
⑸ unsupervised hierarchical clustering vs K-means clustering
| Unsupervised Hierarchical Clustering | K-means Clustering | |
|---|---|---|
| Time Complexity | O(n3) | O(kn) × iteration |
| Randomness | Deterministic | Random |
Table. 1. Comparison of unsupervised hierarchical clustering and K-means clustering
⑹ K-NN vs K-means clustering
| Item | K-NN | K-means Clustering |
|---|---|---|
| Type | Supervised Learning | Unsupervised Learning |
| Meaning of k | Number of Nearest Neighbors | Number of Clusters |
| Optimization Techniques | Cross Validation, Confusion Matrix | Elbow Method, Silhouette Method |
| Application | Classification | Clustering |
Table 2. K-NN vs K-means clustering
4. Type 3. Density-Based Clustering (DBSCAN, density-based spatial clustering of applications with noise)
⑴ Overview: One of the non-hierarchical clustering analyses like K-means clustering
① An algorithm that groups closely distributed entities based on the calculation of their densities
② No need to pre-specify the number of clusters
③ Clusters are connected based on cluster density, allowing for clustering of geometric shapes
⑵ Components
① Core point
○ A data point that has a minimum number(min_samples) of other data points within a certain radius(epsilon)
○ The minimum number of data points required within the radius is set as a hyperparameter
② Neighbor point
○ Other data existing within a certain radius around a specific data point
③ Border point
○ Not a core point but exists within the radius of a core point
○ Included in the cluster centered around the core point and typically forms the outskirts of the cluster
④ Noise point
○ Neither a core point nor satisfies the border point condition
○ Also considered as an outlier
⑶ Procedure
① Stage 1. Identify core points with a minimum number(min_samples) of points within a certain radius(epsilon).
② Stage 2. Explore connected components in the adjacency graph using only core points.
③ Stage 3. Assign non-core points as noise.
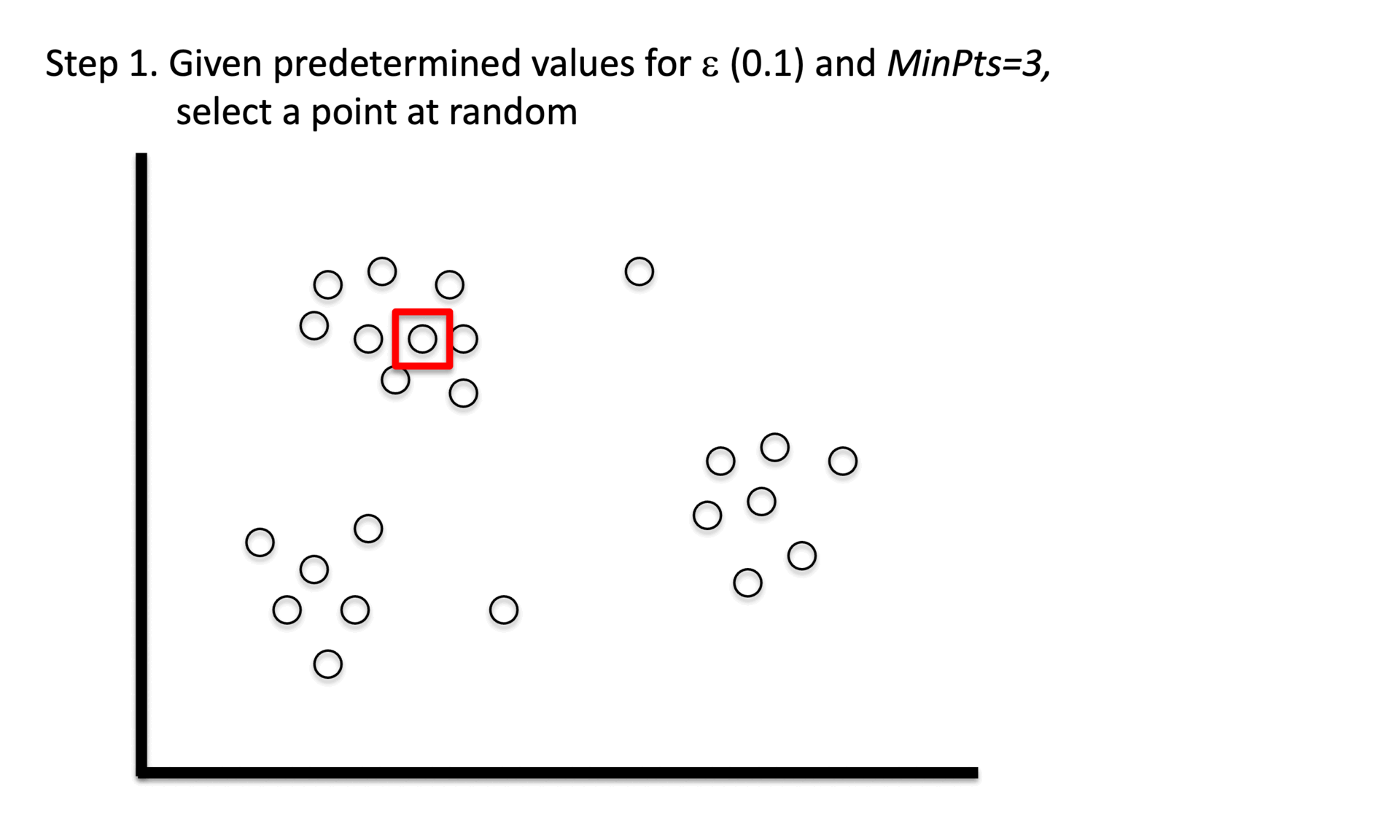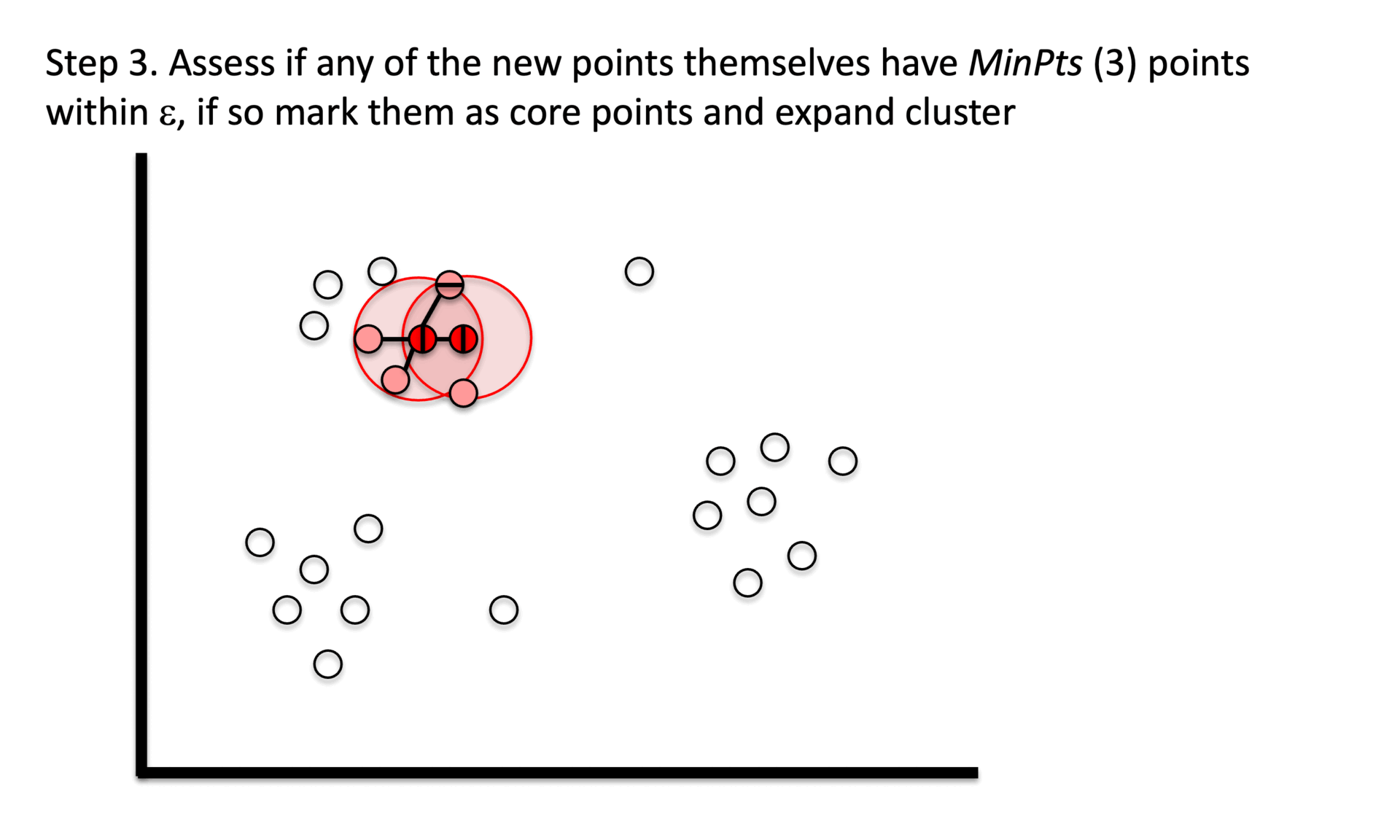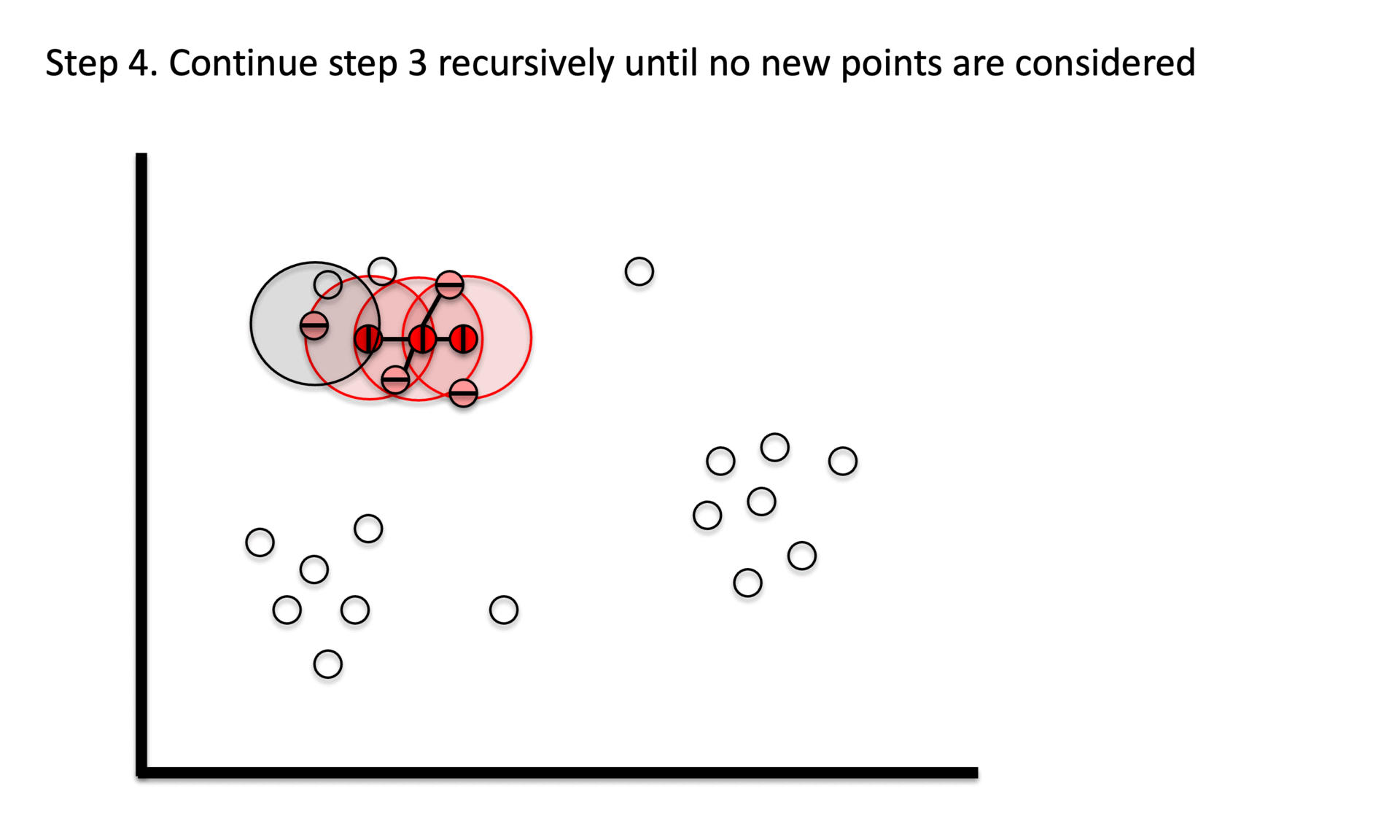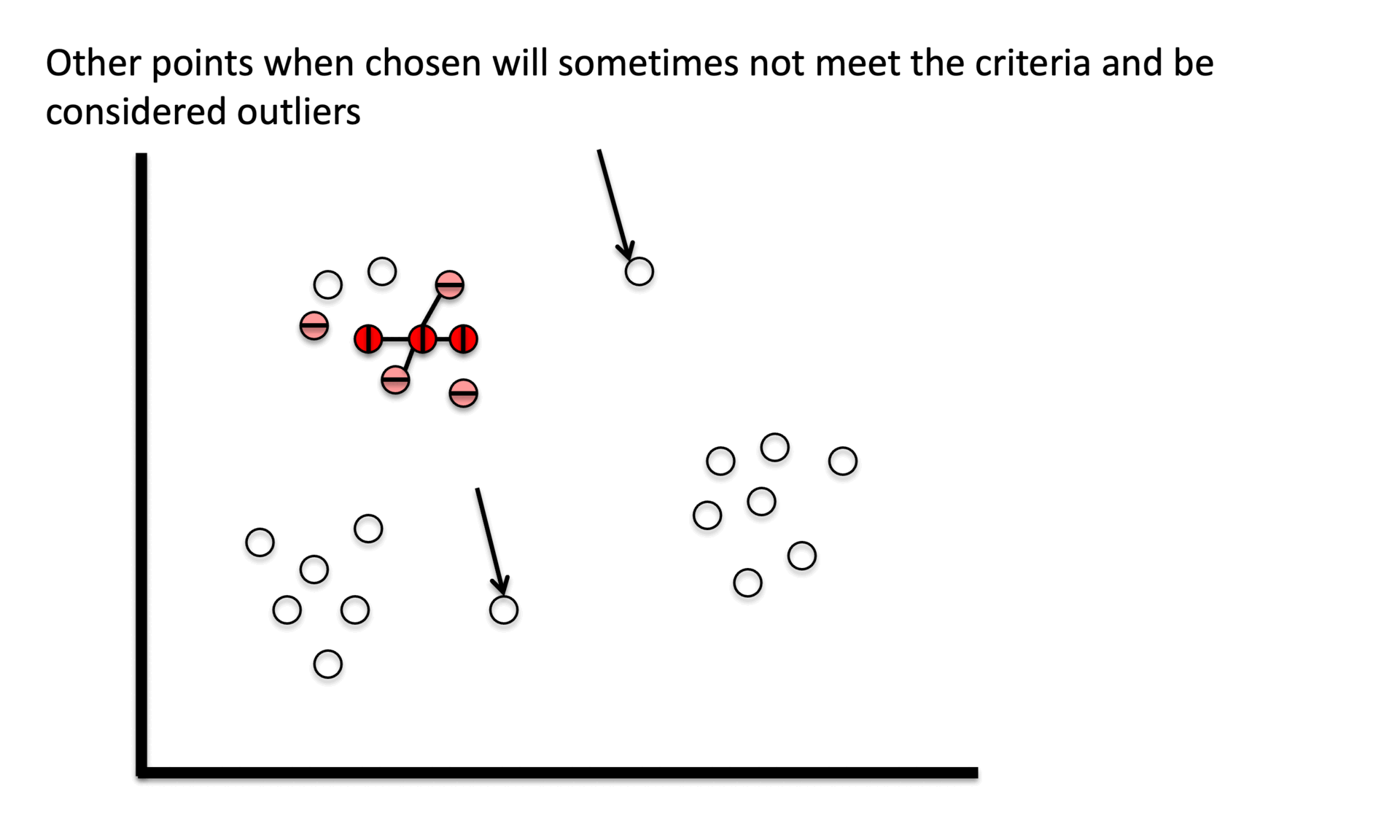
Figure 6. Gibbs Sampling initialization
⑷ Features
① Advantage 1. No need to predefine the number of clusters, unlike K-means clustering
② Advantage 2. Can identify clusters with geometric shapes due to clustering based on cluster density
③ Disadvantage 1. Difficult to determine hyperparameters, sensitive to parameter choices
④ Disadvantage 2. Challenges in computation when clusters have varying densities or in higher dimensions
⑸ Python example
Figure 7. DBSCAN Python example
import pandas as pd
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
# Step 1: Generate sample data
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# Step 2: Convert to DataFrame
df = pd.DataFrame(X, columns=['x', 'y'])
# DBSCAN parameters
epsilon = 0.5
min_samples = 5
# Step 3: Perform DBSCAN clustering
db = DBSCAN(eps=epsilon, min_samples=min_samples)
df['cluster_label'] = db.fit_predict(df[['x', 'y']])
# Step 4: Visualize the clustering results
plt.figure(figsize=(12, 8))
plt.scatter(df['x'], df['y'], c=df['cluster_label'], cmap='viridis', marker='o')
plt.title('DBSCAN Clustering')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
⑹ Application
① OPTICS
(skip)
from sklearn.cluster import OPTICS
# OPTICS parameters
min_samples = 5
xi = 0.05
min_cluster_size = 0.05
# Perform OPTICS clustering
optics = OPTICS(min_samples=min_samples, xi=xi, min_cluster_size=min_cluster_size)
df['cluster_label'] = optics.fit_predict(df[['x', 'y']])
(skip)
② HDBSCAN
(skip)
import hdbscan
# HDBSCAN parameters
min_cluster_size = 5
min_samples = 5
# Perform HDBSCAN clustering
hdb = hdbscan.HDBSCAN(min_cluster_size=min_cluster_size, min_samples=min_samples)
df['cluster_label'] = db.fit_predict(df[['x', 'y']])
(skip)
③ DBSCAN++
5. Type 4. Mixture Distribution Clustering
⑴ Mixture Distribution Clustering: One of the non-hierarchical clustering analyses, like K-means clustering
① Assumes data comes from a population model represented as a weighted sum of M parametric models, estimates parameters and weights from the data
② Each of the M models represents a cluster, and each data point is classified into a cluster based on which model it most likely came from
③ Definition of Mixture Model: A mixture model represented as a weighted sum of M distributions (components)
p(x | θ) = Σ p(x | Ci, θi) p(Ci)
○ p(x Ci, θi): The individual probability density function in the mixture model
○ θi: The parameter vector of the i-th distribution
○ Ci: The i-th cluster (class)
○ p(Ci): The importance or weight (αi) of the i-th cluster in the mixture model
④ Estimating parameters of the mixture model is complex compared to single models, often using the EM algorithm instead of differentiation
⑤ Accuracy of estimation may decrease or become challenging if the size of clusters is too small
⑥ Sensitive to outliers, hence preprocessing such as outlier removal is necessary
⑵ Gaussian Mixture Model (GMM)
Figure 8. Gaussian Mixture Model
① Overview
○ Assumes the overall data probability distribution is a linear combination of k Gaussian distributions.
○ Clusters are formed based on the probability of belonging to each distribution.
○ Each feature that makes up the data needs to be bi-modal or multi-modal for it to work well. (ref)
② Formula
○ In GMM, estimates the weights, means, and covariances of the appropriate k Gaussian distributions for the given data X = {x1, x2, …, xN}
○ Simplification: When x is one-dimensional data
○ Matrix Representation: When x is multi-dimensional data, for the mean μk and covariance matrix ∑k of the k-th cluster
③ EM algorithm (MLE estimation)
○ EM algorithm can be used to estimate the optimal Gaussian distribution each data point belongs to
○ Objective function: Expressed as log likelihood
○ Step 1: Assign random values to γi,k
○ Step 2: E-step: Estimate γi,k
○ Step 3: M-step: Calculate ak, μk, ∑k from γi,k
○ Step 4: If γi,k converges, stop; otherwise, move to Step 2: Convergence is guaranteed due to the characteristics of the Gaussian function.
④ Comparison between K means clustering and Gaussian mixture model
Figure 9. Comparison of K means clustering and Gaussian mixture model
6. Type 5. Graph-Based Clustering (SOM, Self-Organizing Maps)
⑴ Overview: One of the non-hierarchical clustering analyses, like K-means clustering
① SOM, developed by Kohonen, also known as Kohonen maps
② SOM is an artificial neural network modeled on the learning processes of the cerebral cortex and visual cortex
③ Clustering by autonomous learning methods
④ A type of unsupervised neural network that maps high-dimensional data into an easy-to-understand low-dimensional arrangement of neurons
⑤ The mapping preserves the positional relationships of input variables
⑥ In the actual space, if input variables are close, they are mapped close to each other on the map
⑦ Very fast due to using only one forward pass
⑵ Type 1. SOM
① Component 1. Input Layer
○ Receives the input vector, contains neurons equal to the number of input variables
○ The input layer data is aligned in the competitive layer through learning, referred to as the map
○ Each neuron in the input layer is fully connected to every neuron in the competitive layer
② Component 2. Competitive Layer
○ A layer arranged in a 2D grid, where input vectors cluster into a single point based on their characteristics
○ SOM uses competitive learning, where each neuron calculates its closeness to the input vector, repeatedly adjusting connection strengths
○ Through the learning process, the connection strength makes the neuron most similar to the input pattern the winner
○ Due to the winner-take-all structure, only the winning neuron appears in the competitive layer, with similar input patterns arranged in the same competitive neuron
③ Learning Algorithm
○ Step 1. Initialization: Initialize connection strengths for nodes in the SOM map
○ Step 2. Input Vector: Present the input vector
○ Step 3. Similarity Calculation: Calculate similarity between the input vector and prototype vectors using Euclidean distance
○ Step 4. Prototype Vector Search: Find the prototype vector (BMU) closest to the input vector
○ Step 5. Strength Readjustment: Readjust the connection strengths of the BMU and its neighbors
○ Step 6. Repeat: Return to step 2 and repeat
⑶ Type 2. Spectral Clustering
① Problem definition
○ Reason why the condition yTDy=1 is necessary: Without this condition, there exists a trivial solution y=0, and for any nonzero y, there exists a scalar c with 0 ≤ 𝑐 < 1 0≤c<1 such that cy makes the objective function arbitrarily small.
○ Reason why the condition yTD1=0 is necessary: This condition is necessary and sufficient for y≠1 (orthogonality). Without it, the minimum of the objective function is always 0 and always achieved at y=1 (by the method of Lagrange multipliers).
② Step 1: Calculate the distance between the given n data points to create an n × n adjacency matrix A.
○ The Gaussian kernel is often used.
③ Step 2: Based on the adjacency matrix, calculate the Laplacian matrix L: Ln or Lr can also be used.
○ L = D - A, where Dii = ∑j Aij
○ Ln = D-1/2LD-1/2 = I - D-1/2AD-1/2
○ Lt = D-1A
○ Lr = D-1L = I - Lt = D-1/2LnD1/2
④ Step 3: Calculate the matrix of eigenvectors W = [ω2, ···, ωk] ∈ ℝn×k corresponding to the k smallest eigenvalues of the Laplacian matrix.
○ The closer the eigenvalue is to 0, the more connected the graph is.
○ Exclude ω1 = 1, which corresponds to λ1 = 0, as it is trivial.
⑤ Step 4: The n data points are naturally embedded into k dimensions: Y = WT = [y1, ⋯, yn], with each column vector representing the embedded data points.
⑥ Step 5: Perform clustering, such as K-means clustering, on the column vectors of Y.
⑷ Type 3. Louvain Clustering: Uses Louvain Modularity Optimization. A type of graph-based method
Figure 10. The principle of Louvain clustering
⑸ Type 4. Kernighan-Lin Algorithm: Uses Pearson correlation maximization.
⑹ Type 5. Stochastic Block Modeling: Uses statistical inference.
⑺ Type 6. Leiden Clustering
① Graph-based clustering method
② The Leiden algorithm used in the scanpy pipeline
import scanpy as sc
import numpy as np
# Load your AnnData object
adata = sc.read_h5ad('my_h5ad.h5ad')
# Run PCA to reduce dimensionality
sc.pp.pca(adata, n_comps=20)
# Compute the neighborhood graph
sc.pp.neighbors(adata)
# Run clustering using the Leiden algorithm (HERE!)
sc.tl.leiden(adata, resolution = 0.5)
# Optionally, compute UMAP for visualization
sc.tl.umap(adata)
# Plotting the results
sc.pl.umap(adata, color='leiden', title='Leiden Clustering')
sc.pl.spatial(adata, color = 'leiden')
7. Other Clustering Algorithms
⑴ SNN (Shared Nearest Neighbor) Modularity Optimization Based Clustering Algorithm
① Step 1. Search for K-nearest neighbors
② Step 2. Construct the SNN graph
③ Step 3. Optimize the modularity function to define clusters
④ Reference Paper: Waltman and van Eck (2013) The European Physical Journal B
⑵ Topic Modeling: LDA, NMF, CountClust (Dey et al., 2017), FastTopics (Carbonetto et al., 2023)
⑶ Mean-Shift Clustering
⑷ NMF (Non-Negative Matrix Factorization)
① Algorithm for decomposing known matrix A into the product of matrices W and H: A ~ W × H
○ A Matrix: Sample-feature matrix, known from samples
○ H Matrix: Variable-feature matrix
○ This helps in extracting metagenes
○ Similar to K means clustering, PCA algorithms
② Algorithm: Searches for U, V which satisfy R = UV, R ∈ ℝ5×4, U ∈ ℝ5×2, and V ∈ ℝ2×4.
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
for i in range(3):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U@V # it is similar to R!
③ NMF(non-negative matrix factorization)
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
for i in range(20):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
V = np.where(V >= 0, V, 0) #set negative entries equal zero
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U = np.where(U >= 0, U, 0) #set negative entries equal zero
U@V # it is similar to R!
④ Matrix completion (such as the Netflix algorithm): A process of applying matrix factorization to a masked version of matrix R.
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
mask=np.array([[1.,1,1,1],
[1,0,0,0],
[1,0,0,0],
[1,0,0,0],
[1,0,0,0]])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
RR = U@V
RR = RR*(1-mask)+R*mask
for i in range(20):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
V = np.where(V >= 0, V, 0)
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U = np.where(U >= 0, U, 0)
RR = U@V
RR = RR*(1-mask)+R*mask
RR*(1-mask)+R*mask # it is similar to R!
⑤ SVD(singular value decomposition)
⑥ Application 1. Cell Type Classification
○ For determining cell type proportion from scRNA-seq obtained from tissue
○ Important to reduce the confounding effect of cell type heterogeneity
○ 1-1. Constrained linear regression
○ 1-2. Reference-based approach
○ 1-2-1. CIBERSORT(cell-type identification by estimating relative subsets of RNA transcript): Allows checking cell type proportion, p value per sample
⑦ Application 2. Joint NMF: Extends to multi-omics
⑧ Application 3. Extracting metagenes
⑨ Application 4. Starfysh: The following describes an algorithm that infers archetypes from spatial transcriptomics data and identifies anchor spots representing each archetype.
○ Step 1. Autoencoder Construction
○ X ∈ ℝS×G: Input data (spots × genes)
○ D: Number of archetypes
○ B ∈ ℝD×S: Encoder. This represents the inference of archetypes. The sum of each archetype’s distribution over all spots should be 1.
○ H = BX: Latent variable
○ W ∈ ℝS×D: Decoder. This reconstructs the input data. The sum of all archetype weights for each spot should be 1.
○ Y = WBX: Reconstructed input
○ Step 2. Solve the optimization problem to compute W and B
○ Step 3. Anchor spots are selected as the spots with the highest weight for each archetype from the W matrix.
○ Step 4. Granularity adjustment: If archetypes are close to each other, they are merged or adjusted using a hierarchical structure.
○ Step 5. For each anchor, the nearest spots are identified to form an archetypal community, and marker genes are explored.
○ Step 6. When a signature gene set is provided, archetypal marker genes are added to the existing gene set, and anchors are recalculated.
○ In this step, the stable marriage matching algorithm is used to pair each archetype with the most similar signature.
⑸ Edge Detection Algorithm
① Type 1. Canny edge detection
○ Step 1. Gaussian blurring
○ Step 2. Find edge gradient strength and direction
○ Step 3. Trace along the edge: If the gradient size is greater than a certain value, the next pixel is selected based on edge direction
○ Step 4. Suppress non-maximum edge: Remove the weak edge parallel to the strong edge
② Type 2. Region-oriented segmentation
○ Step 1. Start with a set of seed points
○ Step 2. From the seed points, grow regions by appending to each seed point the neighboring pixels that have similar properties.
○ Drawbacks: Selection of seed points, Selection of appropriate parameters, Lack of stopping rules
Figure 11. Region-oriented segmentation (Note that T = 3 means the cutoff of the difference in values)
③ Type 3. Region splitting and merging
○ Step 1. Split an image into four disjoint quadrants.
○ Step 2. Merge any similar adjacent regions.
○ Step 3. Stop when no further merging or splitting is possible.
○ Drawback: Takes a long time, but can be alleviated by parallel computing.
Figure 12. region splitting and merging
① **An algorithm to identify ROI in images based on threshold values like certain brightness levels
⑺ Thresholding Method
① Definition: A technique to create a binary image based on a threshold
② Example: Otsu Thresholding Method
⑻ MST (Minimum Spanning Tree)
⑼ Curve Evolution
⑽ Sparse Neighboring Graph: A type of graph-based method
⑾ SC3
⑿ SIMLR
⒀ FICT
⒁ Faiss
① A similarity-based search and dense vector clustering algorithm developed by Meta in 2023.
② Fast search algorithm: capable of obtaining the nearest neighbor and the k-th nearest neighbor.
③ Allows for the search of multiple vectors at once (batch processing).
④ There is a trade-off between accuracy and speed.
⑤ Instead of minimizing Euclidean distance, it calculates by maximizing the maximum inner product.
⑥ Returns all elements contained within a given radius.
⒂ mclust
⒃ PAM clustering
⒄ Affinity propagation: Provided by scikit package
⒅ BIRCH: Provided by scikit package
Entered: 2021.11.16 13:17
Edited: 2025.04.02 00:20